Alguns subconjuntos de \(\mathbb{R}^n\)

Vamos ilustrar os conceitos revistos sobre \(\mathbb{R}^n\) para dar exemplos de alguns conjuntos particularmente importantes e caracterizá-los geometricamente. Citaremos várias definições e resultados de Álgebra Linear sem demonstração.

Rectas, planos, subespaços

Dado um vector \(\boldsymbol{u}\in\mathbb{R}^n\) a recta com a direcção de \(\boldsymbol{u}\) e passando pela origem, \(\boldsymbol{0}\), é o conjunto \[\{\alpha\boldsymbol{u}:\alpha\in\mathbb{R}\}.\]

Dados vectores \(\boldsymbol{u},\boldsymbol{v}\in\mathbb{R}^n\) a recta com a direcção de \(\boldsymbol{u}\) e passando por \(\boldsymbol{v}\) é o conjunto \[\{\boldsymbol{v}+\alpha\boldsymbol{u}:\alpha\in\mathbb{R}\}.\]

Dados vectores \(\boldsymbol{u},\boldsymbol{v}\in\mathbb{R}^n\) o segmento de recta unindo \(\boldsymbol{v}\) a \(\boldsymbol{v}+\boldsymbol{u}\) é o conjunto \[\{\boldsymbol{v}+\alpha\boldsymbol{u}:\alpha\in [0,1]\}.\]

Dado um vector \(\boldsymbol{u}\in\mathbb{R}^n\), unitário, isto é verificando \(\|\boldsymbol{u}\|=1\), e um vector \(\boldsymbol{v}\in\mathbb{R}^n\), a distância de \(\boldsymbol{v}\) à recta passando pela origem com a direcção de \(\boldsymbol{u}\) é \[\|\boldsymbol{v}-(\boldsymbol{v}\cdot\boldsymbol{u})\boldsymbol{u}\|\] ou seja a norma da diferença entre \(\boldsymbol{v}\) e a sua projecção sobre a recta.

Exercício. Verifique que a afirmação anterior é coerente com a definição de distância de um ponto a um subconjunto de $\mathbb{R}^n$.

Dado um número finito de vectores de \( \mathbb{R}^n\), \(\boldsymbol{v}_1,\dots \boldsymbol{v}_k\), o subespaço de \( \mathbb{R}^n\) gerado por estes vectores é o conjunto \[\left\{ \sum_{j=1}^{k} \alpha_j  \boldsymbol{v}_j\in\mathbb{R}^n: ( \alpha_1,\dots,\alpha_k)\in\mathbb{R}^k\right\}.\]

Tal conjunto é um subespaço vectorial de \(\mathbb{R}^n\) de dimensão \(\leq k\). Se os vectores \(\boldsymbol{v}_j\) forem linearmente independentes o espaço gerado tem dimensão \(k\) e diz-se que os \(\boldsymbol{v}_j\) formam uma base desse subespaço. É sempre possível, através do procedimento de Gram-Schmidt, obter, a partir de uma qualquer base de um subespaço de $\mathbb{R}^n$, uma base ortonormada, isto é formada por vectores de norma 1 e ortogonais entre si.

Dados um subespaço $S$ de dimensão $d$ de $\mathbb{R}^n$ com uma base ortonormada $\{\boldsymbol{u}_j\}_{j=1,\dots,d}$ e um vector $\boldsymbol{v}\in\mathbb{R}^n$, a projecção de $\boldsymbol{v}$ sobre $S$ é \[P(\boldsymbol{v})=\sum_{j=1}^d (\boldsymbol{u}_j\cdot\boldsymbol{v})\boldsymbol{u}_j.\]

Exercício. Verifique que a distância de um ponto $\boldsymbol{v}$ a um subespaço $S$, nas condições descritas atrás, é $\|\boldsymbol{v} - P(\boldsymbol{v})\|$. Este exercício generaliza o anterior.

Se adicionarmos um vector fixo a todos os elementos de um subespaço vectorial de dimensão \(k\) obtemos um subespaço afim do espaço vectorial que diremos também de dimensão \(k\). Aos subespaços afins de dimensão \(1\) em \(\mathbb{R}^n\)chamaremos rectas, aos subespaços afins de dimensão \(2\) chamaremos planos e aos subespaços de dimensão \(n-1\) chamaremos hiperplanos.

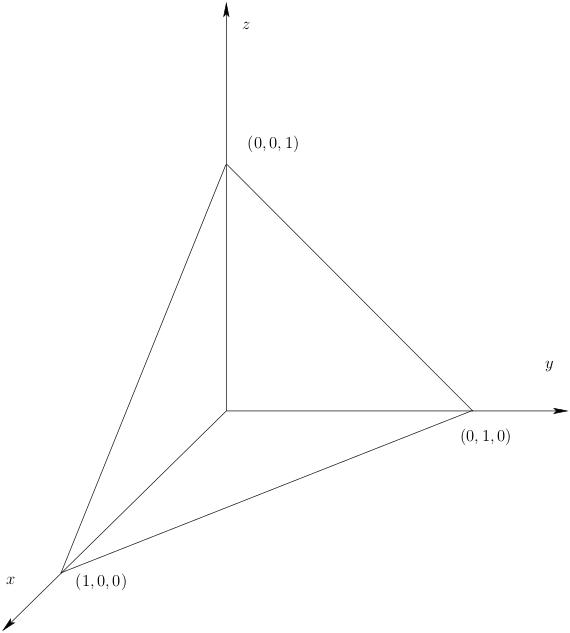
Exemplo. O conjunto \(\left\{(x,y,z)\in\mathbb{R}^3: x+y+z=1\right\}\) é um subespaço afim de dimensão $2$ em \(\mathbb{R}^3\) que geometricamente designamos como um plano. Uma maneira prática de visualizar este plano é notar que as suas intersecções com os eixos coordenados são os pontos \((1,0,0)\), \((0,1,0)\), \((0,0,1)\).

Superfícies

Iremos considerar subconjuntos de $\mathbb{R}^n$ que têm, perto de cada um dos seus pontos e num sentido a precisar quando estudarmos variedades, o carácter de um subespaço afim “deformado” de dimensão $k$ com $0\lt k \lt n$.

Dado \(\boldsymbol{a}\in\mathbb{R}^n\) e \(r\gt 0\) a esfera de raio \(r\) centrada em \(\boldsymbol{a}\) é o conjunto \[\partial B_r(\boldsymbol{a})=\left\{\boldsymbol{x}\in\mathbb{R}^n:\|\boldsymbol{x}-\boldsymbol{a}\|=r\right\}.\]

Dado um vector \(\boldsymbol{u}\in\mathbb{R}^n (n\geq 3)\), unitário, isto é verificando \(\|\boldsymbol{u}\|=1\), e um número real \(c\gt 0\), o cilindro cujo eixo é a recta que passa por \(\boldsymbol{0}\) com a direcção de \(\boldsymbol{u}\) e com raio \(c\) em \(\mathbb{R}^n\) é dado por \[\left\{\boldsymbol{x}\in\mathbb{R}^n:\|\boldsymbol{x}-(\boldsymbol{x}\cdot\boldsymbol{u})\boldsymbol{u}\|=c\right\}.\] No caso particular de \(n=3\), \(\boldsymbol{u}=(0,0,1)\) e \(c=1\) a equação do cilindro seria \[x^2+y^2=1.\]

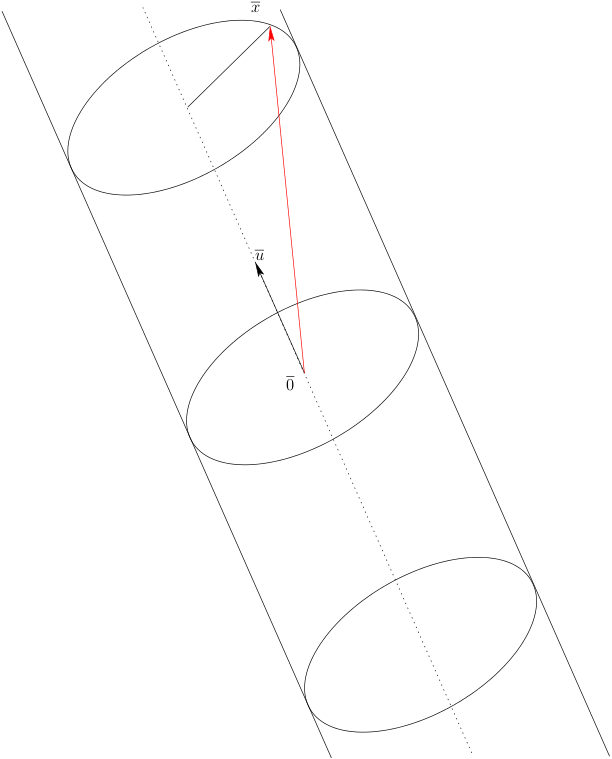
De forma análoga, se a norma de \( \boldsymbol{x}-(\boldsymbol{x}\cdot\boldsymbol{u})\boldsymbol{u} \) não for constante, mas tiver outro tipo de comportamento, podemos obter outras superfí­cies, que já devem ser familiares, em \(\mathbb{R}^n\). Por exemplo se for proporcional a \(|\boldsymbol{x}\cdot \boldsymbol{u}|\) obtemos um cone. Mais precisamente se \(\alpha\gt 0\) for a constante de proporcionalidade\[ \left\{\boldsymbol{x}\in\mathbb{R}^n:\|\boldsymbol{x}-(\boldsymbol{x}\cdot\boldsymbol{u})\boldsymbol{u}\|=\alpha|\boldsymbol{x}\cdot \boldsymbol{u}|\right\}.\]

Obtemos um parabolóide de forma análoga com \[\left\{\boldsymbol{x}\in\mathbb{R}^n:{\|\boldsymbol{x}-(\boldsymbol{x}\cdot\boldsymbol{u})\boldsymbol{u}\|}^2=\alpha{(\boldsymbol{x}\cdot \boldsymbol{u})}\right\}.\]

Obtemos um hiperboloide (de revolução) se considerarmos \[\left\{\boldsymbol{x}\in\mathbb{R}^n:{\|\boldsymbol{x}-(\boldsymbol{x}\cdot\boldsymbol{u})\boldsymbol{u}\|}^2-{(\boldsymbol{x}\cdot \boldsymbol{u})}^2 = \pm 1\right\}.\] O hiperboloide terá uma ou duas folhas (a razão destas designações deve ser óbvia olhando para as figuras) consoante o sinal no segundo membro da igualdade.

Bolas

Introduzimos notação especial para conjuntos que designaremos como bolas, abertas ou fechadas, por omissão abertas, em \(\mathbb{R}^n\).

Definição (Bola (aberta), bola fechada). A bola (aberta) de raio \( r \gt 0 \) e centrada em \(\boldsymbol{a}\in\mathbb{R}^n\) é o conjunto \[ B_r(\boldsymbol{a})=\{\boldsymbol{x}\in\mathbb{R}^n: \|\boldsymbol{x}-\boldsymbol{a}\|\lt r\}.\]

De forma análoga a correspondente bola fechada é o conjunto \[ \overline{B}_r(\boldsymbol{a})=\{\boldsymbol{x}\in\mathbb{R}^n: \|\boldsymbol{x}-\boldsymbol{a}\|\leq r\}. \]

Note-se que $\overline{B}_r(\boldsymbol{a}) \setminus B_r(\boldsymbol{a})= \partial B_r(\boldsymbol{a})$.

A importância destes conjuntos resulta de os dois primeiros irem desempenhar o papel das vizinhanças de um ponto de \(\mathbb{R}\) ao generalizarmos as noções de limite, continuidade, etc. A nomenclatura e notação serão coerentes com o que faremos quando introduzirmos noções topológicas em \(\mathbb{R}^n\).

Definição (Conjunto limitado). Um subconjunto de $\mathbb{R}^n$ diz-se limitado se existir uma bola que o contém.

Exercício. Mostre que uma caracterização equivalente de conjunto limitado é existir uma bola centrada em $\boldsymbol 0$ que o contém.

A acção de translações e transformações lineares sobre subconjuntos de \(\mathbb{R}^n\)

Um tema recorrente ao lidarmos com subconjuntos de \(\mathbb{R}^n\) será utilizar aplicações de \(\mathbb{R}^n\) em \(\mathbb{R}^n\) particularmente simples para relacionar conjuntos conhecidos com outros. Os dois exemplos mais simples de tal prática correspondem a translações e transformações lineares com ênfase nalguns casos particulares destas últimas como rotações ou homotetias.

A translação por um vector \(\boldsymbol{h}\in\mathbb{R}^n\) é a aplicação \[\mathbb{R}^n\ni \boldsymbol{x}\mapsto \tau_{\boldsymbol{h}}(\boldsymbol{x})=\boldsymbol{x}+\boldsymbol{h}. \]

Note que se um conjunto é descrito na forma \[\{\boldsymbol{x}\in\mathbb{R}^n: F(\boldsymbol{x})=\boldsymbol{0}\}\] para alguma função \(F\) então o seu transladado por \(\boldsymbol{h}\) tanto pode ser descrito por \[\{\boldsymbol{x}+\boldsymbol{h}\in\mathbb{R}^n: F(\boldsymbol{x})=\boldsymbol{0}\}\] ou \[\{\boldsymbol{x}\in\mathbb{R}^n: F(\boldsymbol{x}-\boldsymbol{h})=\boldsymbol{0}\}.\]

Por exemplo, se transladarmos o parabolóide descrito por \(z=x^2+y^2\) pelo vector \((1,2,-1)\) obtemos o parabolóide descrito por \(z+1=(x-1)^2+(y-2)^2\).

Se \(T:\mathbb{R}^n\to \mathbb{R}^n\) for uma transformação linear invertível será frequente, dado um subconjunto de \(\mathbb{R}^n\) caracterizado por \(\{\boldsymbol{x}\in\mathbb{R}^n: F(\boldsymbol{x})=\boldsymbol{0}\}\), considerar o transformado \(\{T\boldsymbol{x}\in\mathbb{R}^n: F(\boldsymbol{x})=\boldsymbol{0}\}\) ou \(\{\boldsymbol{x}\in\mathbb{R}^n: F(T^{-1}\boldsymbol{x})=\boldsymbol{0}\}\). Casos particularmente frequentes correspondem a \(T\) ser uma homotetia (\(T\boldsymbol{x}=\alpha \boldsymbol{x}\) para algum \(\alpha\neq 0\)), \(T\) ser representado por uma matriz diagonal, ou \(T\) ser uma rotação, isto é, ter a sua transposta como inversa e determinante \(1\) (\(TT^t=T^tT=I\), \(\det T=1\)).

A última figura ilustra estas transformações começando com uma circunferência de raio \(1\) centrada em \((0,0)\) que é transformada sucessivamente numa elipse de semi-eixos de comprimento \(1\) e \(1/2\), paralelos às bissectrizes dos quadrantes do plano e centrada em \((1,1)\).

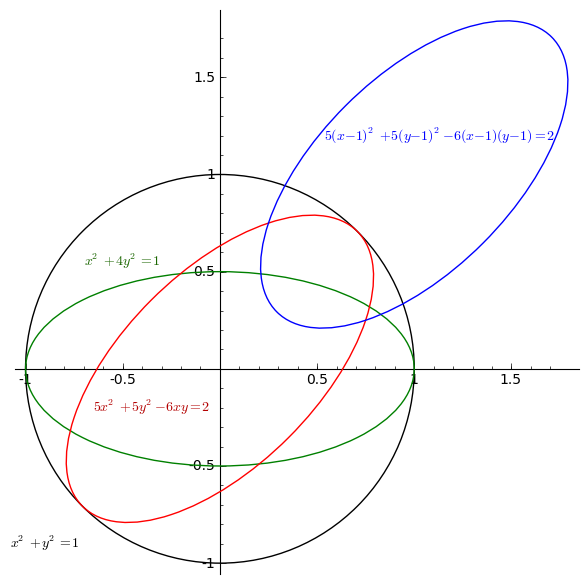
Exercício. Determine as transformações usadas para obter as equações na figura Círculo e elipses.

Exercício. Verifique, a partir da definição de rotação, que todas as rotações no plano são representadas por matrizes reais \(2\times 2\) da forma \[\begin{bmatrix}\cos \theta & -\operatorname{sen}\theta \\ \operatorname{sen}\theta & \cos\theta\end{bmatrix}\] para algum $\theta\in\mathbb{R}$. Fim de enunciado de exercício.

Para compreender rotações em \(\mathbb{R}^3\) um primeiro passo talvez deva ser o

Teorema (Euler). Seja \(R\) uma rotação em \(\mathbb{R}^n\) com \(n\) ímpar. Então existe um vector \(\boldsymbol{x}\) de \(\mathbb{R}^n\) tal que \(R\boldsymbol{x}=\boldsymbol{x}\).

Ideia da demonstração. Sendo \(I\) a aplicação linear identidade, tente mostrar que \(\det(R-I)=0\) e consequentemente um valor próprio de \(R-I\) é \(0\), o que implica a conclusão.

Assim, as rotações em \(\mathbb{R}^3\) são rotações em torno de um eixo.