Continuidade global
Teorema do valor intermédio
O teorema do valor intermédio para funções reais de varíável real afirma que uma função contínua definida num intervalo tem como contradomínio um intervalo. Ao pretender generalizar este resultado a funções definidas em subconjuntos de $\mathbb{R}^n$ com valores em $\mathbb{R}^m$ a questão se põe é saber qual é a classe de subconjuntos de $\mathbb{R}^n$ que poderão substituir os intervalos de $\mathbb{R}$ naquele enunciado. Nitidamente considerar intervalos seria restritivo demais.
Definição (conjunto desconexo). $S\subset\mathbb{R}^n$ diz-se desconexo se existirem subconjuntos não vazios $A$ e $B$ de $S$ tais que $A\cup B=S$, $A\cap \overline{B}=\emptyset = \overline{A}\cap B$. Diremos que $A$ e $B$ separam $S$.
Note que, se $S$, como na definição anterior, é desconexo e $A$ e $B$ separam $S$, então a função $f:S\to\mathbb R$ definida por \[f(\boldsymbol{x})=\begin{cases}1,& \text{ se } \boldsymbol{x}\in A, \\ 0, & \text{ se } \boldsymbol{x}\in B.\end{cases}\] é uma função contínua em $S$ cujo contradomínio não é um intervalo. Isto porque se $\boldsymbol{x}_0\in A$ não há, de certeza, sucessões de termos em $B$ que convirjam para $\boldsymbol{x}_0$ e, de forma idêntica, o mesmo acontece trocando $A$ com $B$, algo que sabemos graças à caracterização dos fechados por sucessões.
Assim, se esperamos generalizar o teorema do valor intermédio, só o conseguiremos fazer para conjuntos que não sejam desconexos. De facto, consegui-lo-emos fazer para todos os conjuntos que não são desconexos.
Exercício. Decida em que casos é que $S\subset\mathbb R^2$ é desconexo:
- $S=B_1(0,0) \cup B_1(3,0)$;
- $S=B_1(0,0) \cup B_1(2,0)$;
- $S=B_1(0,0) \cup \overline{B}_1(2,0)$.
Definição (conjunto conexo). Se $S\subset\mathbb{R}^n$ não é desconexo diz-se conexo.
Proposição Os subconjuntos conexos de $\mathbb{R}$ são os intervalos.
Demonstração. Suponha-se que $S\subset\mathbb{R}$ não é um intervalo. Então existem $a,b\in S$ e $c\not\in S$ tais que $a\lt c\lt b$. Sejam $A={]{-\infty}, c[}\cap S$ e $B={]c,+\infty[}\cap S$. Tais conjuntos $A$ e $B$ separam $S$, isto é, $S$ não é conexo.
Suponha-se que $S\subset\mathbb{R}$ é um intervalo e não é conexo. Então existiriam $A\subset S$ e $B\subset S$ que separam $S$. Suponha-se, sem perda de generalidade, que existem pontos $a\in A$ e $b\in B$ tais que $a\lt b$. Seja $c=\sup\{x\in A: x\lt b \}$. Nitidamente $c\in \overline{A}$. Seja $d=\inf\{x\in B: c \lt x\lt b\}$. Não podemos ter $d\gt c$ pois $S$ é um intervalo. Logo $c=d$ e $c\in \overline{B}$. Como $S$ é um intervalo $c\in A$ ou $c\in B$. Mas então ou $\overline{A}\cap B\neq \emptyset$ ou $A\cap \overline{B}\neq \emptyset$ o que contradiz $A$ e $B$ separarem $S$. Portanto se $S$ é um intervalo então é conexo. Fim da demonstração.
Não é óbvio como identificar todos os conjuntos que designamos como conexos. Uma condição suficiente de fácil verificação envolve o conceito de conjunto conexo por arcos.
Definição (Conjunto conexo por arcos). $A\subset\mathbb{R}^n$ diz-se conexo por arcos se dados dois quaisquer pontos $\boldsymbol{x}, \boldsymbol{y}\in A$ existir uma aplicação contínua $r:[0,1]\to A$ tal que $r(0)=\boldsymbol{x}$ e $r(1)=\boldsymbol{y}$.
Note que em geral chama-se arco ou caminho a uma aplicação contínua definida num intervalo de $\mathbb{R}$ com valores em $\mathbb{R}^n$. Os arcos são usados nas aplicações à física para modelar trajectórias de partículas, calcular trabalho realizado num campo de forças, etc. Voltaremos a este tema quando discutirmos linhas e integrais de linha.
Proposição. Os conjuntos conexos por arcos são conexos.
Ideia da demonstração. Seja $S$ conexo por arcos mas não conexo, separado por dois conjuntos $A$ e $B$. Considere um caminho $r$ unindo um ponto de $A$ a um ponto de $B$ e as imagens inversas por $r$ de $A\cap r([0,1])$ e $B\cap r([0,1])$. Estas imagens inversas separariam $[0,1]$ mas já vimos que um intervalo é conexo. Fim da ideia de demonstração.
Note que é trivial que a imagem de um conjunto conexo por arcos por uma função contínua é conexo por arcos graças ao teorema de continuidade da função composta. Tal permite-nos, para exemplos relativos simples, tirar conclusões sobre o contradomínio de uma função com valores reais.
Exemplo. Voltemos a considerar \(f:T\subset \mathbb{R}^2\to \mathbb{R}\) com \(T=\{(x,y)\in \mathbb{R}^2: x\geq 0, y\geq 0, x+y\leq 1\}\) e \(f(x,y)=x^2 y^3(1-x-y)\).
Já verificámos que esta função possui um máximo em $T$ que ocorre no ponto $(1/3,1/2)$ e um mínimo $0$ que ocorre em todos os pontos de $\partial T$. Dado que $T$ é conexo por arcos, ou muito trivialmente considerando a restrição de $f$ ao segmento de recta unindo $(0,1/2)$ a $(1/3,1/2)$, a continuidade de $f$ permite garantir que o contradomínio é um intervalo que, tomando em conta a informação já conhecida, terá que ser $[0,f(1/3,1/2)]$. Fim de exemplo.
Para funções reais cujo domínio não seja conexo por arcos mas seja conexo poderemos necessitar de um resultado mais forte para realizar o mesmo tipo de análise:
Teorema (do valor intermédio). Seja $S\subset\mathbb{R}^n$ um conjunto conexo e $f:S\to \mathbb{R}^m$ uma função contínua. Então o contradomínio de $f$, $f(S)$, é um conjunto conexo.
Demonstração. A demonstração repete um raciocínio similar ao que já usámos para sugerir que um conexo por arcos é conexo. Suponha-se que dois conjuntos não vazios $A$ e $B$ separam o contradomínio de $f$. Então temos $S=f^{-1}(A)\cup f^{-1}(B)$, $f^{-1}(A)\neq \emptyset$, $f^{-1}(B)\neq \emptyset$ e $f^{-1}(A) \cap f^{-1}(B)=\emptyset$. Para concluir precisamos mostrar que também \[f^{-1}(A) \cap\overline{ f^{-1}(B)}=\emptyset=\overline{f^{-1}(A)}\cap f^{-1}(B).\] Suponha-se, sem perda de generalidade, que $\boldsymbol{x}\in f^{-1}(A) \cap\overline{ f^{-1}(B)}$. Então $f(\boldsymbol{x})\in A$ e existe uma sucessão $(\boldsymbol{x}_k)$ tal que $\boldsymbol{x}_k\to \boldsymbol{x}$ e, para todo o $k$, $f(\boldsymbol{x}_k)\in B$. Mas, usando continuidade à Heine, $f(\boldsymbol{x}_k)\to f(\boldsymbol{x})$ mostrando que $f(\boldsymbol{x})\in \overline{B}$. Logo $A\cap \overline{B}\supset\{f(\boldsymbol{x})\}\neq \emptyset$ o que contradiria $A$ e $B$ separarem o contradomínio de $f$. Fim de demonstração.
Convém convencer o leitor de que o teorema anterior contém de facto mais informação do que aquilo que trivialmente obteríamos para conexos por arcos exibindo um conjunto conexo que não é conexo por arcos.
Exercício. Seja $S=\left\{(x,y)\in\mathbb{R}^2: y=\operatorname{sen}\left(\frac{1}{x}\right), x\gt 0\right\}\cup \{(0,0)\}$. Mostre que $S$ é conexo mas não conexo por arcos.
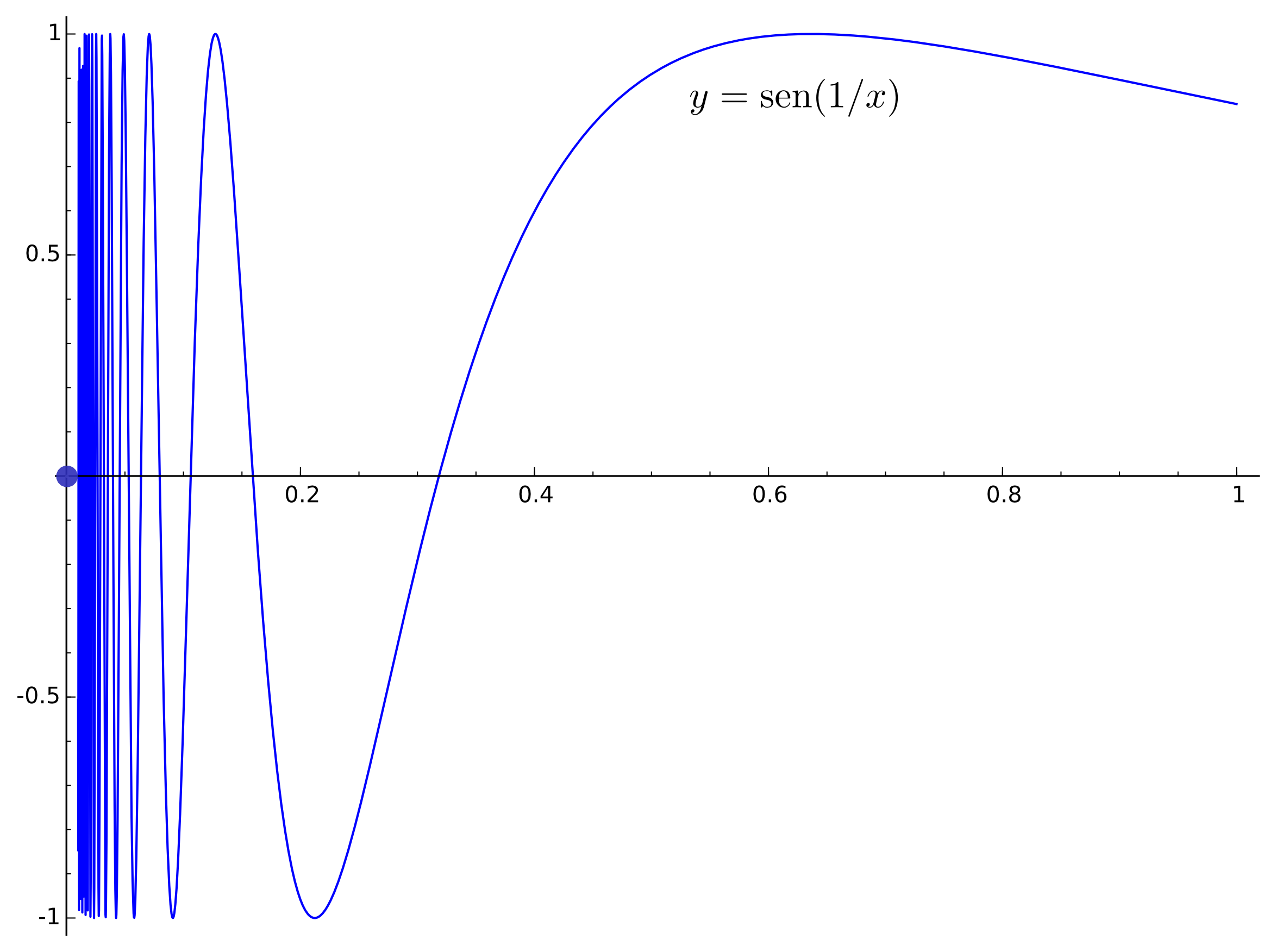
Esboço de solução do exercício.
Começamos por provar que $S$ é conexo. Se $S$ fosse desconexo existiriam $A,B\subset S$ com $A\neq \emptyset\neq B$, $A\cup B=S$ e $\overline{A}\cap B = \emptyset = \overline{B}\cap A$. Seja $S^+=\{(x,y)\in S: x\gt 0\}$. Se $A\cap S^+\neq \emptyset \neq B\cap S^+$ teríamos que $S^+$ seria desconexo. Tal é uma contradição pois $S^+$ é conexo por arcos e portanto conexo. Assim, ou $A=S^+$ e $B=\{(0,0)\}$, ou $B=S^+$ e $A=\{(0,0)\}$. Tal no entanto também é impossível pois $(0,0)\in \overline{S^+}$.
Para mostrar que $S$ não é conexo por arcos, suponha-se que existe uma aplicação $r:[0,1]\to S$, contínua tal que $r(0)\in S^+$ e $r(1)=(0,0)$. Note-se que se convencionarmos $r(t)=(x(t),y(t))$ temos sempre \[y(t)=\begin{cases}\sen(1/x(t)), & \text{se } x(t)\gt 0 \\ 0, & \text{se } x(t)=0.\end{cases}\]
Seja $t^\ast=\inf \{t\in [0,1]: r(t)=(0,0)\}$. Como $r$ é contínua, $r(t^\ast)=(0,0)$. Além disso, por continuidade de $x(\cdot)$, temos $t^\ast\gt 0$. Desta forma a restrição de $r$ a $[0,t^\ast]$ é contínua e $r([0,t^\ast[)\subset S^+$.
Aplicando a definição de continuidade em $t^\ast$, existe $\delta\gt 0$ tal que se $t\in{]t^\ast-\delta, t^\ast[}$ temos $0\lt\sqrt{x(t)^2+ y(t)^2}\lt 1/2$ e, em particular, $|y(t)|=|\sen (1/x(t))|\lt 1/2$ donde, para cada $t\in{]t^\ast-\delta, t^\ast[}$ devemos ter $1/x(t)\in {]k\pi-\frac{\pi}{6}, k\pi+\frac{\pi}{6}[}$ para algum $k\in\mathbb{N}$. Tal acarreta que existe uma recta definida por $x=1/(k\pi+ \pi/2)$ com $k\in\mathbb{N}$ que não intersecta $r(]t^\ast-\delta, t^\ast[)$ e tal que que existem pontos de $r(]t^\ast-\delta, t^\ast[)$ à sua direita e à sua esquerda. Mas então $r(]t^\ast-\delta, t^\ast[)$ não seria conexo (por arcos) que constitui a contradição que estabelece que $S$ não pode ser conexo por arcos.
Há, no entanto, uma importante classe de conjuntos para a qual os conceitos de conexo e conexo por arcos coincidem.
Proposição (Abertos conexos são conexos por arcos). Se $S\subset\mathbb{R}^n$ é um conjunto aberto então $S$ é conexo se e só se é conexo por arcos.
Ideia da demonstração. Já sabemos que se $S$ é conexo por arcos então é conexo.
Suponha que $S$ é conexo e aberto e não é conexo por arcos. Se $S$ não é conexo por arcos existem pontos $\boldsymbol{a},\boldsymbol{b}\in S$ tais que não existe um caminho unindo $\boldsymbol{a}$ a $\boldsymbol{b}$. Sejam \[\begin{align*}A & = \{\boldsymbol{x}\in S: \text{Existe um caminho unindo } \boldsymbol{a} \text{ a } \boldsymbol{x}. \} \\ B & = \{\boldsymbol{x}\in S:\text{Não existe um caminho unindo } \boldsymbol{a} \text{ a } \boldsymbol{x}.\}\end{align*}\] Temos $\boldsymbol{a}\in A$ e $\boldsymbol{b}\in B$ pelo que estes conjuntos são não vazios. Além disso $A\cup B=S$. Acontece que tanto $A$ como $B$ são conjuntos abertos. Para justificar a afirmação anterior no caso de $A$ (para $B$ o argumento é análogo) note que sendo $S$ aberto e $\boldsymbol{x}\in A$ existe $r\gt 0$ tal que $B_r(\boldsymbol{x})\subset S$. Dois quaisquer pontos de $B_r(\boldsymbol{x})$ podem ser unidos por um segmento de recta. Assim, dado um $\boldsymbol{z}\in B_r(\boldsymbol{x})$ podemos construir um caminho que une $\boldsymbol{a}$ a $\boldsymbol{z}$ concatenando o caminho que une $\boldsymbol{a}$ a $\boldsymbol{x}$ com o segmento de recta que une $\boldsymbol{x}$ a $\boldsymbol{z}$. Este argumento prova que $A$ é um conjunto aberto.
Para concluir a demonstração mostre que $A\cap \overline{B} = \emptyset = B\cap \overline{A}$ (graças a $A$ e $B$ serem abertos) e que portanto $A$ e $B$ separariam $S$ o que contradiz este ser conexo. Fim da ideia de demonstração.
Uma ideia usada na justificação do resultado anterior fornece um critério geométrico simples para dar exemplos adicionais de conjuntos conexos.
Definição (Conjunto convexo). Um conjunto $C\subset\mathbb{R}^n$ diz-se convexo se quaisquer que sejam $\boldsymbol{x}, \boldsymbol{y}\in C$ o segmento de recta unindo $\boldsymbol{x}$ a $\boldsymbol{y}$ estiver contido em $C$.
Proposição. Uma bola em $\mathbb{R}^n$ é um conjunto convexo.
Ideia da demonstração. Use a desigualdade triangular. Fim da ideia de demonstração.
Proposição (Convexidade implica conectividade). Os subconjunto convexos de $\mathbb{R}^n$ são conexos.
Ideia da demonstração. Dados quaisquer dois pontos do conjunto parametrize o segmento de recta que os une para provar que o conjunto é conexo por arcos. Fim da ideia de demonstração.
Também consideraremos uma outra classe particular de conexos por arcos, os conjuntos em estrela.
Definição (Conjunto em estrela) Um conjunto $C\subset\mathbb{R}^n$ diz-se em estrela se existir um ponto $\boldsymbol{x}_0\in C$ tal que qualquer que seja o $\boldsymbol{x}\in C$ o segmento de recta unindo $\boldsymbol{x}_0$ a $\boldsymbol{x}$ estiver contido em $C$.
Obviamente todos os conjuntos convexos são em estrela mas o recíproco não é verdadeiro.
Exercício. Mostre que $B_2(\boldsymbol{0})\setminus B_1(\boldsymbol{0})$ é conexo mas não é convexo.
Exercício. Este exercício formaliza a ideia de concatenar caminhos referida atrás. Dado um caminho $\alpha$ unindo os pontos $\boldsymbol{x}$ a $\boldsymbol{y}$ e um caminho $\beta$ unindo os pontos $\boldsymbol{y}$ a $\boldsymbol{z}$ explicite, em termos de $\alpha$ e $\beta$ um caminho $r$ unindo $\boldsymbol{x}$ a $\boldsymbol{z}$.
Exercício. Sejam $L_1$, $L_2$ e $L_3$ respectivamente os segmentos de recta em $\mathbb{R}^2$ unindo $(0,0)$ a $(1,1)$, $(0,0)$ a $(1,-1)$ e $(0,0)$ a $(-1,0)$. Mostre que não existe uma aplicação injectiva e contínua definida em $L_1\cup L_2\cup L_3$ com valores em $\mathbb{R}$.
Esboço de solução. Se tal aplicação existisse transformaria cada $L_i$ num intervalo não reduzido a um ponto. Os três intervalos assim obtidos deveriam ter um ponto comum, a imagem de $(0,0)$. A injectividade da aplicação mostra que tal não é possível. Fim do esboço de solução.
Exercício. Seja $\alpha:[0,1]\to\mathbb{R}^n$ uma aplicação contínua e injectiva. Seja $L=\alpha([0,1])$. Mostre que qualquer outra aplicação $\beta:[0,1]\to L$ contínua e injectiva verificando $\beta([0,1])=L$ ou verifica $\alpha(0)=\beta(0)$ e $\alpha(1)=\beta(1)$, ou verifica $\alpha(0)=\beta(1)$ e $\alpha(1)=\beta(0)$.
Exercício. Mostre que um aberto é conexo por arcos se e só se for conexo por arcos poligonais.
Última edição desta versão: João Palhoto Matos, 05/10/2023 17:41:35.
