Cálculo de integrais em limitados de $\mathbb{R}^n$ via integrais iterados usando coordenadas cartesianas

Assumindo que uma função é integrável num intervalo limitado de \(\mathbb{R}^n\) vamos ver ver que é fácil perceber porquê e como reduzimos o cálculo a sucessivas integrações de funções de uma variável em intervalos limitados de \(\mathbb{R}\). Como protótipo de uma tal situação consideremos uma função \(f:[0,1]^2\to\mathbb{R}\) integrável no sentido que temos vindo a estudar. Gostaríamos de saber se é legítimo proceder ao cálculo via \[\iint_{[0,1]^2}f=\int_0^1\left(\int_0^1 f(x,y) \, dx\right)\, dy\] (a resposta, algo surpreendente, vai ser uma versão rigorosa de "nem sempre, mas quase sempre") no que constitui o análogo infinitesimal de, por exemplo, somar os elementos de uma matriz primeiro por linhas e depois somar a coluna dos totais parciais, i.e., \[\sum_{ij}a_{ij} = \sum_j\left(\sum_i a_{ij}\right)\]

Além disso verificaremos que há várias estratégias de como organizar o cálculo, mais ou menos convenientes conforme a geometria do problema.

Como integrar: o teorema de Fubini

O resultado básico sobre cálculo de integrais baseia-se em comparar cuidadosamente somas superiores e inferiores da função com somas superiores e inferiores de outra função que corresponde de alguma forma a já ter-se integrado em relação a algumas variáveis.

Suponhamos que \(f:I=I_1\times I_2\to\mathbb{R}\) é uma função integrável em \(I\) um intervalo limitado e fechado de \(\mathbb{R}^n\). Numa primeira leitura suponha que \(n=2\) e que \(I_1\) e \(I_2\) são intervalos de \(\mathbb{R}\) mas em geral serão um intervalo de \(\mathbb{R}^k\) e um intervalo de \(\mathbb{R}^{n-k}\) para um certo \(k < n\). Dado um qualquer \(\epsilon \gt 0\), existe uma partição \(P\in\mathcal{P}(I)\) tal que \[S(f,P)-s(f,P)\lt\epsilon.\]

A partição \(P\) em \(\mathbb{R}^n\) pode ser descrita via \(P=P_1\times P_2\) em que \(P_j\in\mathcal{P}(I_j)\), \(j=1,2\). Convencionamos que os subintervalos definidos por \(P\) designam-se \(I_{\alpha\beta}=I_\alpha\times I_\beta\) em que os \(I_\alpha\) são os subintervalos de \(I_1\) determinados por \(P_1\) e os \(I_\beta\) são os subintervalos de \(I_2\) determinados por \(P_2\). Convencionamos também escrever os vectores de \(\mathbb{R}^n\) na forma \((\boldsymbol{x},\boldsymbol{y})\) com \(\boldsymbol{x}\in\mathbb{R}^k\), \(\boldsymbol{y}\in\mathbb{R}^{n-k}\).

A comparação de somas superiores consiste em \begin{align*}S(f,P) & \texttip{=}{definição de soma superior}\sum_{\alpha,\beta}\sup_{I_{\alpha\beta}}f\operatorname{vol}(I_{\alpha\beta})\mathtip{=}{\operatorname{vol}(I_{\alpha\beta}) = \operatorname{vol}(I_{\alpha})\operatorname{vol}(I_{\beta})}\sum_{\alpha}\left(\sum_{\beta}\sup_{I_{\alpha\beta}}f\operatorname{vol}(I_{\beta})\right) \operatorname{vol}(I_{\alpha}) \\ & \mathtip{= }{\sup_{x,y}g(x,y)=\sup_x\sup_y g(x,y)}\sum_{\alpha}\left(\sum_{\beta}\sup_{\boldsymbol{x}\in I_{\alpha}}\left(\sup_{\boldsymbol{y}\in I_{\beta}}f(\boldsymbol{x},\boldsymbol{y})\right)\operatorname{vol}(I_{\beta})\right) \operatorname{vol}(I_{\alpha}) \\ & \mathtip{\geq}{\sup f + \sup g \geq \sup(f+g)} \sum_{\alpha}\sup_{\boldsymbol{x}\in I_{\alpha}}\left(\sum_{\beta}\left(\sup_{\boldsymbol{y}\in I_{\beta}}f(\boldsymbol{x},\boldsymbol{y})\right)\operatorname{vol}(I_{\beta})\right)\operatorname{vol}(I_{\alpha}) \\ & \texttip{\geq}{definição de integral superior}\sum_{\alpha}\sup_{\boldsymbol{x}\in I_{\alpha}}\overline{\int_{I_2}}f(\boldsymbol{x},\boldsymbol{y})\, d\boldsymbol{y}\operatorname{vol}(I_{\alpha}) \texttip{=}{definição de soma superior} S(g,P_1)\end{align*} em que a função $g$ no último membro é definida por \(g(\boldsymbol{x})=\overline{\int_{I_2}}f(\boldsymbol{x},\boldsymbol{y})\, d\boldsymbol{y}\).

De forma análoga para as somas inferiores \begin{align*}s(f,P) & \texttip{=}{definição de soma inferior} \sum_{\alpha,\beta}\inf_{I_{\alpha\beta}}f\operatorname{vol}(I_{\alpha\beta})\mathtip{=}{\operatorname{vol}(I_{\alpha\beta}) = \operatorname{vol}(I_{\alpha})\operatorname{vol}(I_{\beta})}\sum_{\alpha}\left(\sum_{\beta}\inf_{I_{\alpha\beta}}f\operatorname{vol}(I_{\beta})\right) \operatorname{vol}(I_{\alpha}) \\ & \mathtip{= }{\inf_{x,y}g(x,y)=\inf_x\inf_y g(x,y)} \sum_{\alpha}\left(\sum_{\beta}\inf_{\boldsymbol{x}\in I_{\alpha}}\left(\inf_{\boldsymbol{y}\in I_{\beta}}f(\boldsymbol{x},\boldsymbol{y})\right)\operatorname{vol}(I_{\beta})\right) \operatorname{vol}(I_{\alpha}) \\ &\mathtip{\leq}{\inf f + \inf g \leq \inf(f+g)} \sum_{\alpha}\inf_{\boldsymbol{x}\in I_{\alpha}}\left(\sum_{\beta}\left(\inf_{\boldsymbol{y}\in I_{\beta}}f(\boldsymbol{x},\boldsymbol{y})\right)\operatorname{vol}(I_{\beta})\right) \operatorname{vol}(I_{\alpha}) \\ & \texttip{\leq}{definição de integral inferior}\sum_{\alpha}\inf_{\boldsymbol{x}\in I_{\alpha}}\underline{\int_{I_2}}f(\boldsymbol{x},\boldsymbol{y})\, d\boldsymbol{y}\operatorname{vol}(I_{\alpha}) \\ & \mathtip{\leq}{\underline{\int}\leq\overline{\int}} \sum_{\alpha}\inf_{\boldsymbol{x}\in I_{\alpha}}\overline{\int_{I_2}}f(\boldsymbol{x},\boldsymbol{y})\, d\boldsymbol{y}\operatorname{vol}(I_{\alpha}) \texttip{=}{definição de soma inferior} s(g,P_1).\end{align*}

As desigualdades que estabelecemos garantem então que também \[S(g,P_1)-s(g,P_1)\lt \epsilon\] donde concluímos que \(g\) é integrável em \(I_1\). Além disso como \[s(f,P)\leq s(g,P_1) \leq S(g,P_1) \leq S(f,P)\] podemos concluir que \[\int_I f = \int_{I_1}\left(\overline{\int_{I_2}}f(\boldsymbol{x},\boldsymbol{y})\, d\boldsymbol{y}\right)\,d\boldsymbol{x}.\]

Com uma ligeira alteração no argumento precedente também se estabelece que \[\int_I f = \int_{I_1}\left(\underline{\int_{I_2}}f(\boldsymbol{x},\boldsymbol{y})\, d\boldsymbol{y}\right)\,d\boldsymbol{x}.\] e obviamente pode-se trocar o papel desempenhado por \(\boldsymbol{x}\) e \(\boldsymbol{y}\) o que resumidamente estabelece

Teorema (de Fubini, cálculo de integrais via integrais iterados.) Seja \(f:J\times K\to \mathbb{R}\) uma função limitada integrável no produto cartesiano de intervalos limitados e fechados \(J\) de \(\mathbb{R}^n\) e \(K\) de \(\mathbb{R}^m\). Então \[\int_{J\times K} f  = \int_J \left(\overline{\int_K}f(\boldsymbol{x},\boldsymbol{y})\, d\boldsymbol{y}\right)d\boldsymbol{x}= \int_J \left(\underline{\int_K}f(\boldsymbol{x},\boldsymbol{y})\, d\boldsymbol{y}\right)d\boldsymbol{x}  = \int_K \left(\overline{\int_J}f(\boldsymbol{x},\boldsymbol{y})\, d\boldsymbol{x}\right)d\boldsymbol{y}=\int_K \left(\underline{\int_J}f(\boldsymbol{x},\boldsymbol{y})\, d\boldsymbol{x}\right)d\boldsymbol{y}.\]

Exemplo. Consideremos \(f:[0,1]^2\to\mathbb{R}\) definida por \(f(x,y)=x^2 y^3\) e o integral \(\iint_{[0,1]^2} f\). Admitindo que sabemos que esta função é integrável (dentro de pouco tempo usaremos o facto da função ser um polinómio de duas variáveis para dizer que é uma função contínua num intervalo limitado e fechado e consequentemente integrável) \[\iint_{[0,1]^2} x^2 y^3 \,dx\,dy= \int_0^1 \left(\int_0^1 x^2y^3\, dx\right)\, dy= \int_0^1 \frac{y^3}{3}\, dy=\frac{1}{12}.\]

[Uma observação sobre notação: aparecer \(dx\,dy\) no primeiro membro da linha anterior não tem qualquer significado sobre a ordem pela qual se procede ao cálculo dos integrais iterados; é simplesmente uma maneira de escrever "fim de integral duplo sendo as variáveis de integração \(x\) e \(y\)", algo que muitas vezes nos será conveniente.]

Exemplo. O exemplo anterior pode ter tornado o leitor algo céptico de que seja de facto preciso considerar integrais superiores e inferiores no enunciado do teorema nesta secção. Vamos ver que de facto tal em geral não é evitável. Seja \(g:[0,1]^2\to\mathbb{R}\) definida por \[g(x,y)=\begin{cases}0, \text{ se } x\neq \frac{1}{2}, \\ 1, \text{ se } x=\frac{1}{2} \text{ e } y\in\mathbb{Q}, \\ -1, \text{ se } x=\frac{1}{2} \text{ e } y\in[0,1]\setminus\mathbb{Q}. \end{cases}\] É fácil verificar que esta função é integrável em \([0,1]^2\) (faça-o!). Neste caso o integral \(\int_0^1g\left(\frac{1}{2},y\right)\, dy\) não existe mas \(\overline{\int_0^1}g\left(\frac{1}{2},y\right)\, dy=1\), \(\underline{\int_0^1}g\left(\frac{1}{2},y\right)\, dy=-1\) e o cálculo pode ser completado de acordo com o teorema fornecendo o valor \(0\) para o integral \(\iint_{[0,1]^2}g\).

Exemplo. Uma outra questão que convém esclarecer para testar os limites do resultado que estabelecemos é saber se da existência de integrais iterados podemos estabelecer a existência do integral original. Seja \(H:[-1,1]^2\to\mathbb{R}\) definida por \[H(x,y)=\begin{cases}0, & \text{ se } x\in\mathbb{Q}, \\ \operatorname{sen}(\pi y), & \text{ se } x\not\in\mathbb{Q}. \end{cases}\] Verifique que \[\int_{-1}^1\left(\int_{-1}^1H(x,y)\,dy\right)dx=0\] mas \(\iint_{[-1,1]^2}H\) não existe.

Exemplo. Voltemos a considerar a função \(f:[0,1]^2\to\mathbb{R}\) definida por \(f(x,y)=x^2 y^3\) mas desta vez consideremos o integral \(\iint_{T} f\). em que \(T=\{(x,y)\in\mathbb{R}^2:x+y\leq 1, x\geq 0, y\geq 0\}\). De acordo com as nossas definições isto corresponde a considerar \(\int_{[0,1]^2}f^\ast\) em que \[f^\ast(x,y)=\begin{cases}f(x,y), & \text{ se } (x,y)\in T, \\ 0, & \text{ se } (x,y)\in[0,1]^2\setminus T.\end{cases}\]

Obtemos então, admitindo integrabilidade, \[\iint_{T} f  = \iint_{[0,1]^2} f^\ast = \int_0^1 \left(\int_0^1 f^\ast(x,y)\,dy\right)\,dx  = \int_0^1 \left(\int_0^{1-x} x^2 y^3 \,dy\right)\,dx = \int_0^1 x^2 \frac{(1-x)^4}{4}\,dx = \int_0^1 \frac{x^2}{4} (1-4x+6x^2-4x^3+ x^4)\,dx = \frac{1}{4} \int_0^1  x^2-4x^3+6x^4-4x^5+ x^6\,dx  = \frac{1}{4}\left( \frac{1}{3}-1+\frac{6}{5}-\frac{2}{3}+\frac{1}{7}\right).\]

De notar que os integrais iterados usados para efectuar o cálculo são um caso particular de \[\iint_A f = \int_{\operatorname{proj}_X(A)}\left(\int_{C_x(A)}f(x,y)\, dy\right)\, dx\] em que \(\operatorname{proj}_X(A)\) é a projecção de \(A\) no eixo dos \(xx\), e \(C_x(A)\) corresponde aos valores de \(y\) determinados pelo "corte" de \(A\) para o valor de \(x\) indicado, isto é, \[\operatorname{proj}_X(A)=\{x\in\mathbb{R}:\exists_y \;(x,y)\in A\}\] e \[C_x(A)=\{y\in\mathbb{R}: (x,y)\in A\}.\]

Fim de exemplo.

Domínios de integração mais complexos que os considerados até agora facilmente podem levar a um volume de cálculos considerável e a considerarmos qual a melhor ordem de integração para proceder aos cálculos.

Exemplo. Seja \(S=\{(x,y)\in\mathbb{R}^2: x\leq y \leq 2x, 1\leq xy \leq 4\}\) e \(h:S\to\mathbb{R}\) definida por \(h(x,y)=\frac{1}{xy}\). Admitindo a integrabilidade de \(h\) em \(S\) vamos calcular \(\iint_S f\).

O conjunto \(S\) é limitado por dois arcos de ramos de hipérbole e dois segmentos de recta como sugerido na figura.

Intersectando \(S\) com rectas horizontais ou com rectas verticais verificamos, tanto num caso como outro que somos conduzidos à soma de três integrais iterados. Por exemplo, considerando que integramos primeiro em ordem a \(x\) somos conduzidos a considerar \[\iint_S h = \int_1^{\sqrt{2}}\left(\int_{\frac{1}{y}}^y \frac{1}{xy} \, dx\right)dy+ \int_{\sqrt{2}}^2 \left(\int_{\frac{y}{2}}^y \frac{1}{xy} \, dx\right)dy+ \int_2^{2\sqrt{2}} \left(\int_{\frac{y}{2}}^\frac{4}{y} \frac{1}{xy} \, dx\right)dy\]

[Complete os cálculos. Resolva considerando a outra possível ordem de integração. Note que voltará a encontrar este problema mais à frente quando dispuser de mudanças de coordenadas, o que poupará consideravelmente a extensão dos cálculos a efectuar.]

Fim de exemplo.

A determinação de limites de integração ao integrar em \(\mathbb{R}^3\) põe algumas questões que em dimensão \(2\) não estão presentes. Começamos por um análogo tridimensional do exemplo do conjunto \(T\).

Exemplo. Considere \(P=\{(x,y,z)\in\mathbb{R}^3: x\geq 0, y\geq 0, z\geq 0, x+y+z\leq 1\}\) e \(g:P\to\mathbb{R}\) definida por \(g(x,y,z)=x y z\) admitindo que \(g\) é integrável em \(P\). Vamos considerar os dois pontos de vista naturais para determinar os limites de integração de integrais iterados. Supondo que optamos por ordem de integração correspondente a considerar sucessivamente integrações em ordem a \(z\), \(y\) e \(x\) podemos começar por considerar \[\iiint_P g = \iint_{\operatorname{proj}_{XY}(P)}\left(\int_{C_{(x,y)}(P)}g(x,y,z)\, dz\right)dx\,dy\] ou \[\iiint_P g= \int_{\operatorname{proj}_X(P)}\left(\iint_{C_x(P)}g(x,y,z)\, dy\,dz\right)dx\] e depois exprimir os integrais duplos como integrais iterados. [Embora o resultado final seja o mesmo o raciocínio será claramente diferente para cada um dos processos não havendo a priori um método mais aconselhável para atacar o problema.] Aqui usámos notações para projecções e cortes na linha do que se já tinha feito atrás em dimensão 2. Em cada uma das linhas seguintes a primeira igualdade corresponde ao que poderia ser a definição formal destes conjuntos e a segunda identifica estes conjuntos neste exemplo \[\begin{align*}\operatorname{proj}_{XY}(P) & =\left\{(x,y)\in\mathbb{R}^2:\exists_{z} (x,y,z)\in P \right\} \\ & =\left\{(x,y)\in\mathbb{R}^2: x\geq 0, y\geq 0, x+y\leq 1 \right\} \\ \operatorname{proj}_{X}(P) & = \left\{x\in\mathbb{R}:\exists_{(y,z)} (x,y,z)\in P \right\}=[0,1]  \\ C_{(x,y)}(P) & = \left\{z\in\mathbb{R}: (x,y,z)\in P \right\}  =[0, 1-x-y ] \\ C_{x}(P) & = \left\{(y,z)\in\mathbb{R}^2: (x,y,z)\in P \right\}\\ & = \left\{(y,z)\in\mathbb{R}^2: y\geq 0, z\geq 0, y+z\leq 1-x \right\} \end{align*} \]

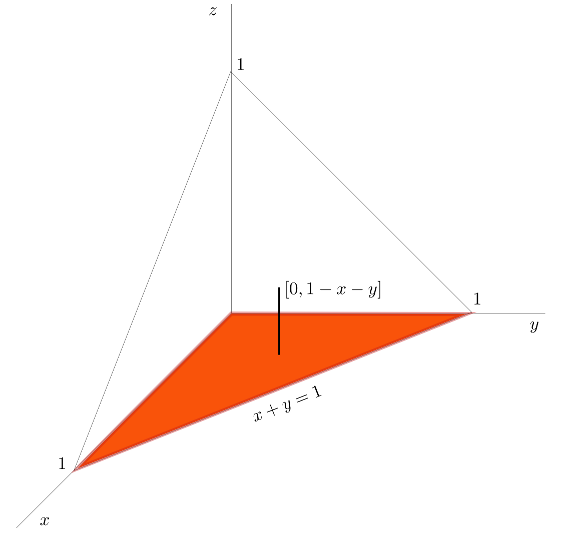
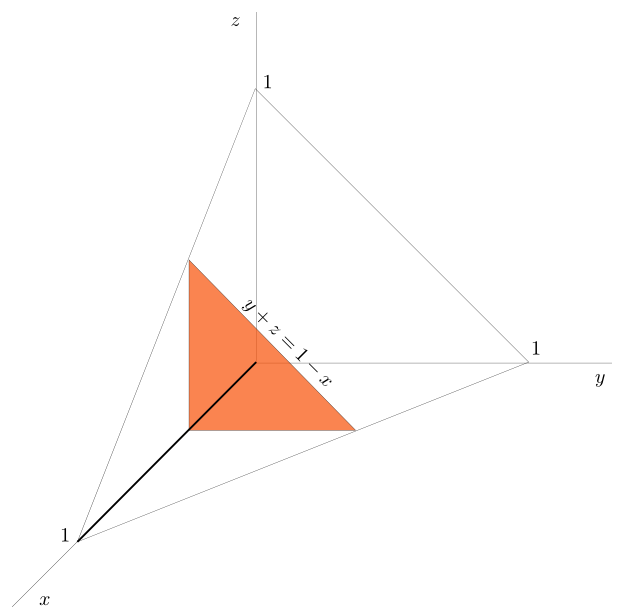
O detalhe dos cálculo da determinação dos limites de integração é, conforme o método aplicado, \[\iiint_P g = \iint_{\{(x,y): \; x\,\geq\,0,\; y\,\geq\,0, \;x+y\,\leq\,1\}}\left(\int_0^{1-x-y} xyz \, dz\right)dx\, dy  = \int_0^1\left(\int_0^{1-x}\left(\int_0^{1-x-y} xyz \, dz\right)dy\right)dx \] \[\iiint_P g  = \int_0^1\left(\int_{\{(y,z)\,\in\,\mathbb{R}^2:\; y\,\geq\,0,\; z\,\geq\,0,\; y+z\,\leq\,1-x\}}xyz\, dy\,dz\right)dx  =\int_0^1\left(\int_0^{1-x}\left(\int_0^{1-x-y} xyz \, dz\right)dy\right)dx\]

[Complete os cálculos.]

Fim de exemplo.

Algo que deverá notar como comum em todos os exemplos anteriores é a necessidade de caracterizar os pontos de $\mathbb R^n$ que possuem, arbitrariamente perto de si, tanto pontos do conjunto onde estamos a integrar como do seu complemento. Aproveitamos para tornar pecisa esta ideia e introduzir alguma terminologia relacionada.

Definição (ponto fronteiro e fronteira). Dado $A\subset \mathbb R^n$ dizemos que $\boldsymbol x_0$ é um ponto fronteiro de $A$ ou pertence à fronteira de $A$, abreviadamente $\boldsymbol x_0\in \partial A$, se qualquer que seja $r\gt 0$, existirem em $B_r(\boldsymbol x_0)$ tanto pontos de $A$ como de $\mathbb R^n\setminus A$.

Volumes $n$-dimensionais

Uma das aplicações básicas da integração é o cálculo do volume de conjuntos $n$-dimensionais: comprimento em $\mathbb{R}$, áreas em $\mathbb{R}^2$, volume em $\mathbb{R}^3$, etc. Deve ser claro da definição de integral que, se $E\subset\mathbb{R}^n$ for um limitado tal que $\int_E 1$ existe, então o valor deste integral é com certeza aquilo que nós queremos designar como volume de $E$. Note que em geral não é legítimo esperar que um conjunto limitado tenha um volume neste sentido como mostra o muito conhecido exemplo $E=\mathbb{Q}\cap [0,1]\subset\mathbb{R}$.

Note que em cursos anteriores não se pôs a questão de calcular o comprimento de conjuntos de $\mathbb{R}$ via integrais pois aí integrávamos em intervalos limitados e nesse caso integrar a função $1$ conduz trivialmente ao comprimento do intervalo.

No caso $n=2$ a sua experiência anterior de calcular áreas consistia quase exclusivamente no cálculo da área de conjuntos da forma $\{(x,y)\in\mathbb{R}^2: x\in [a,b], g(x)\leq y \leq f(x)\}$ em que $a\lt b$ e $f,g:[a,b]\to\mathbb{R}$ são integráveis em $[a,b]$ e tais que $g(x)\leq f(x)$ para todo o $x\in [a,b]$. Admitindo que a função $1$ é integrável em tais conjuntos, algo que demonstraremos com facilidade posteriormente, o teorema de Fubini mostra que \[\iint_{\{(x,y)\in\mathbb{R}^2: x\in [a,b], g(x)\leq y \leq f(x)\}} 1\, dx\,dy = \int_a^b\left(\int_{g(x)}^{f(x)} 1 \, dy\right)\, dx = \int_a^b f(x) - g(x) \, dx\] obtendo-se o processo de cálculo de áreas conhecido.

Note que as propriedades já conhecidas do integral dão-lhe propriedades que espera com certeza que a noção de volume tenha. Nomeadamente, sendo $E\subset\mathbb{R}^n$ um limitado tal que o volume $\int_E 1$ existe, então:

• O volume é sempre maior ou igual a $0$. Tal decorre trivialmente da definição de integral.
• Também decorre da definição de integral que se $E$ contém um intervalo da forma $[a_1, b_1]\times\dots\times [a_n, b_n]$ com $a_k\lt b_k$ para cada $k$ com $1\leq k\leq n$ então o volume de $E$ é minorado por $(b_1-a_1)\dots(b_n-a_n)\gt 0$.
• O volume é invariante por translacção, isto é, se $\boldsymbol{z}\in \mathbb{R}^n$ e $E_{\boldsymbol{z}}=\{\boldsymbol{x}+\boldsymbol{z}: \boldsymbol{x}\in E\}$, então também podemos definir o volume de $E_{\boldsymbol{z}}$ e este é igual ao volume de $E$. Uma forma de obter este resultado neste momento envolve usar o teorema de Fubini e a invariância por translacção do integral em intervalos limitados de $\mathbb{R}$.

A última propriedade que citámos e outras, como a invariância por rotação da noção de volume, estabelecer-se-ão mais facilmente quando dispusermos da fórmula de mudança de variáveis na integração.

Fazemos também notar que temos uma propriedade de aditivade de volumes que decorre da aditividade do integral relativamente à região de integração. Mais precisamente, se pudermos definir o volume de um número finito de subconjuntos de $\mathbb{R}^n$ disjuntos dois a dois, então também podemos definir o volume da união de tais conjuntos e o respectivo volume obtém-se por adição.

Exemplo. Considere a região de $\mathbb{R}^3$ definida pela intersecção dos cilindros definidos por $x^2+y^2\leq 1$ e $y^2+z^2\leq 1$.

Para calcular o volume desta região usando integração pela ordem $z,x,y$ podemos considerar \[\begin{align*}& \iint_{\{x^2+y^2\leq 1\}} \left(\int_{-\sqrt{1-y^2}}^{\sqrt{1-y^2}} \, dz\right)dx\, dy \\ &\qquad = 2\iint_{\{x^2+y^2\leq 1\}}\sqrt{1-y^2} \,dx\,dy \\ &\qquad = 2 \int_{-1}^1 \left(\int_{-\sqrt{1-y^2}}^{\sqrt{1-y^2}}\sqrt{1-y^2}\, dx\right)dy \\ & \qquad = 4 \int_{-1}^1  1-y^2 \, dy = 4\left(2 - \frac{2}{3}\right)= \frac{16}{3}.\end{align*}\]

Exercício. Retome o exemplo anterior determinando os integrais necessários para calcular o volume usando diferentes ordens de integração.

Exemplo (Volume de um tetraedro $n$-dimensional). Este último exemplo destina-se em parte a tentar convencer o leitor de que também é possível realizar cálculos em dimensão $n$ qualquer, embora sem o auxílio dos esboços a que frequentemente recorremos em dimensão $2$ ou $3$.

Sendo $s\geq 0$ e $n\in\mathbb{N}_1$, definimos $V(n,s)$ como sendo o volume $n$-dimensional de \[T(n,s)=\left\{\boldsymbol{x}=(x_i)_{i=1,\dots,n}\in\mathbb{R}^n: x_i \geq 0 \text{ para todo o }i=1,\dots,n, \sum_{i=1}^n x_i\leq s\right\}.\] Vamos provar que $V(n,s)= \frac{s^n}{n!}$ usando indução matemática, o teorema de Fubini e uma mudança de variável unidimensional.

Para $n=1$ temos $V(1,s)=\int_0^s 1 dx_1=s$, verificando o resultado para $n=1$.

Suponhamos que o resultado é válido para dimensão $n-1$. Em dimensão $n$ temos, introduzindo a mudança de variável $x_1=s(1-t_1)$, usando o teorema de Fubini e a hipótese de indução \begin{align*}V(n,s)&=\int_0^s \left( \int_{x_2+...+x_n\leq s-x_1}\, dx_2\dots dx_n\right)\, dx_1 \\ &= s \int_0^1 \left( \int_{x_2+...+x_n\leq s t_1}\, dx_2\dots dx_n \right)dt_1 \\ & = s\int_0^1 V(n-1,st_1) \, dt_1 \\ & = \frac{s^n}{(n-1)!} \int_0^1 t_1^{n-1} \, dt_1  \\ & = \frac{s^n}{n!},\end{align*} completando a demonstração por indução. Fim do exemplo.

O integral permite o cálculo de inúmeras outras grandezas em mecânica dos meios contínuos, electromagnetismo e outras áreas de aplicação das ciências e da engenharia. Por exemplo, se $m(x,y,z) \gt 0$ designa a massa específica de um sólido $V\subset\mathbb{R}^3$ então a massa do sólido será \[\iiint_V m(x,y,z) \, dx\,dy\,dz.\]

Podemos também integrar funções com valores vectoriais (em $\mathbb{R}^d$) definindo o integral da forma natural coordenada a coordenada o que conduz a aplicações como o cálculo do centro de massa de um sólido de massa específica $m(x,y,z)$ via \[\frac{\iiint_V \boldsymbol{r}\, m(x,y,z) \, dx\,dy\,dz}{\iiint_V m(x,y,z) \, dx\,dy\,dz}\] em que $\boldsymbol{r}=(x,y,z)$. No caso de sólidos homogéneos, isto é, com densidade constante, o centro de massas designa-se por centróide.

Exemplo (Centróide do tetraedro). Calculemos as coordenadas do tetraedro que designámos atrás por $T(3,1)$, isto é de $T=T(3,1)=\{(x,y,z)\in\mathbb{R}^3: x+y+z\leq 1, x\geq 0, y\geq 0, z\geq 0\}$.

Notando que permutações de $x$, $y$ e $z$ deixam o conjunto invariante facilmente concluímos que as 3 coordenadas do centróide são iguais. Além disso já calculámos o volume que é igual a $1/6$.

Resta-nos então calcular \begin{align*}\iiint_T x \, dx \, dy\, dz & = \int_0^1 \left( \int_0^{1-x}\left(\int_0^{1-x-y}x\, dz\right)dy\right)\, dx \\ & = \int_0^1 \left( \int_0^{1-x}  x-x^2 - xy \, dy\right)\, dx  \\ & = \int_0^1 ( x-x^2) (1-x) - \frac{x}{2}(1-x)^2 \, dx \\ & = \int_0^1 \frac{x}{2}(1-x)^2 \, dx \\ & = \frac{1}{2} \int_0^1 x -2x^2 + x^3 \, dx = \frac{1}{24}. \end{align*}

Assim o centróide é o ponto com coordenadas $(1/4, 1/4, 1/4)$. Fim de exemplo.