Integrais de linha
A motivação primária para o conceito de integral de linha é o conceito de trabalho num campo de forças. Dada uma função $F:A\subset\mathbb{R}^n\to \mathbb{R}^n$, que daqui para a frente designaremos também por campo vectorial, cujo domínio $A$ é um aberto, e um caminho $r:[a,b]\to A$, o trabalho realizado ao deslocar uma partícula de $r(a)$ para $r(b)$ seria aproximável por \[\sum_{i=0}^k F(r(t_i))\cdot(r(t_{i+1})-r(t_i)) \approx \sum_{i=0}^k F(r(t_i))\cdot r'(t_{i})(t_{i+1}-t_i) \] em que $P=\{t_0=a,t_1,\dots,t_k=b\}\in \mathcal{P}([a,b])$. Tal sugere:
Definição (Integral de linha). Dado um campo vectorial contínuo $F:A\subset\mathbb{R}^n\to \mathbb{R}^n$ com $A$ um aberto e um caminho $r:[a,b]\to A$, $r$ seccionalmente de classe $C^1([a,b])$, definindo uma linha $L=r([a,b])$, define-se o integral de linha de $F$ relativamente ao caminho $r$ como sendo \[\int_L F\cdot dr=\int_a^b F(r(t))\cdot r'(t)\, dt.\]

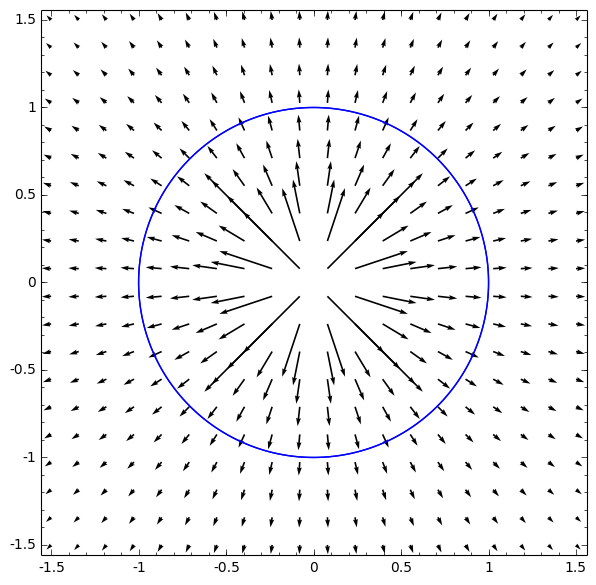
Exemplo. Considere o campo vectorial $F:\mathbb{R}^2\setminus\{(0,0)\}\to \mathbb{R}^2$ definido por \[F(x,y)=\left(\frac{x}{x^2+y^2}, \frac{y}{x^2+y^2}\right)\] e o caminho $\alpha(t)=(\cos t, \operatorname{sen}t)$, $t\in [0,2\pi]$, $S^1=\alpha([0,2\pi])$. Temos $F(\alpha(t))=(\cos t, \operatorname{sen}t)$ e $\alpha'(t)=(-\operatorname{sen}t, \cos t)$ donde $F(\alpha(t))\cdot \alpha'(t)=0$ e \[\int_{S^1} F\cdot d\alpha =0.\] Note que o cálculo simplesmente concretiza tratar-se de um campo radial relativamente a $(0,0)$ e portanto, em cada ponto de $S^1$, ortogonal ao respectivo espaço tangente.
Fim de exemplo.
Convém fazer duas observações sobre notação que vêm a propósito do exemplo anterior:
- Quando consideramos caminhos fechados será por vezes conveniente dar ênfase a esse facto usando notação como \[\oint_{S^1} F\cdot d\alpha .\]
- Quando, como no caso do exemplo anterior, o integral de linha não depende do caminho usado para percorrer a linha, podemos abandonar a menção expressa do caminho usando notação que “explicita” a coordenadas do campo, como \[\oint_{S^1} P\, dx + Q\, dy \] para o integral de linha de um campo com funções coordenadas $(P,Q)$ ou mesmo \[\oint_{S^1} \frac{x}{x^2+y^2}\, dx + \frac{y}{x^2+y^2}\, dy. \]
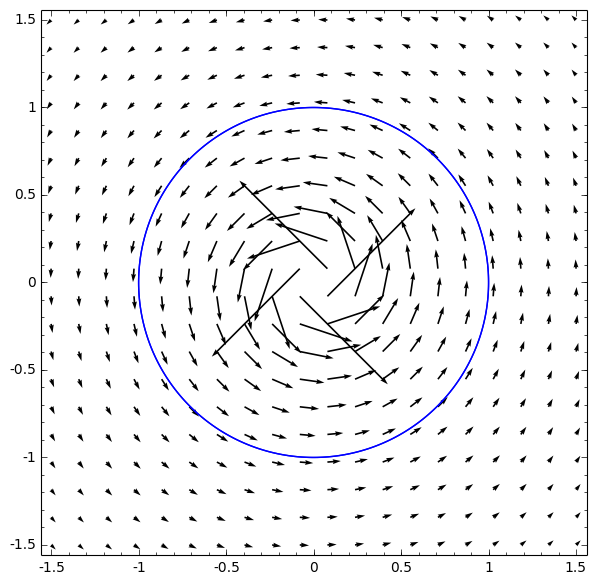
Exemplo. Considere o campo vectorial $G:\mathbb{R}^2\setminus\{(0,0)\}\to \mathbb{R}^2$ definido por \[G(x,y)=\left(\frac{-y}{x^2+y^2}, \frac{x}{x^2+y^2}\right)\] e o caminho $\alpha$ do exemplo anterior. Neste caso \[\oint_{S^1}G\cdot d\alpha =\int_0^{2\pi}\operatorname{sen}^2 t +\cos^2 t\, dt = 2\pi. \] Geometricamente tal corresponde ao campo vectorial ser tangente à circunferência $x^2+y^2=1$ com uma projecção sobre a recta que é constante (igual a $1$).
Fim de exemplo.
Exercício. Prove que se pode estimar um integral de linha usando um integral em ordem ao comprimento de arco na forma \[\left|\int_L F\cdot dr\right| \leq \int_L \|F\|\, ds.\] Fim de exercício.
Embora um integral de linha dependa não só da linha mas também da forma como esta é parametrizada, a dependência em relação à parametrização limita-se, no caso de caminhos seccionalmente $C^1$ injectivos, ao “sentido” em que a linha é percorrida.
Proposição. Seja $F:A\subset\mathbb{R}^n\to \mathbb{R}^n$ com $A$ um aberto um campo vectorial contínuo e $\alpha:[a,b]\to A$, $\beta:[c,d]\to A$ dois caminhos seccionalmente de classe $C^1$ tais que existe uma função $u:[a,b]\to[c,d]$, seccionalmente de classe $C^1$ e com $u'>0$ sempre que a derivada esteja definida, tal que $u([a,b])=[c,d]$ e $\alpha(t)=\beta(u(t))$ para $t\in[a,b]$. Então \[\int_L F\cdot d\alpha = \int_L F\cdot d\beta. \]
Ideia da demonstração. Basta considerar o caso em que $\alpha, \beta, u\in C^1$ nos seus domínios. Note que com as hipóteses que fizemos $u(a)=c$ e $u(b)=d$. \[\begin{align*}\int_L F\cdot d\alpha= &\int_a^b F(\alpha(t))\cdot \alpha'(t)\, dt \\ = & \int_a^b F(\beta(u(t)))\cdot \beta'(u(t))u'(t)\, dt \\ = & \int_c^d F(\beta(s))\cdot \beta'(s)\, ds = \int_L F\cdot d\beta\end{align*}\] em que na segunda igualdade usou-se o teorema de derivação da função composta e na terceira integrou-se por substituição. Fim da ideia da demonstração.
Claro que quando percorremos a mesma linha em “sentido contrário” a relação entre os integrais de linha já não é de igualdade mas sim de simetria.
Proposição. Seja $F:A\subset\mathbb{R}^n\to \mathbb{R}^n$ com $A$ um aberto um campo vectorial contínuo e $\alpha:[a,b]\to A$, $\beta:[c,d]\to A$ dois caminhos seccionalmente de classe $C^1$ tais que existe uma função $u:[a,b]\to[c,d]$, seccionalmente de classe $C^1$ e com $u'<0$ sempre que a derivada esteja definida, tal que $u([a,b])=[c,d]$ e $\alpha(t)=\beta(u(t))$ para $t\in[a,b]$. Então \[\int_L F\cdot d\alpha = -\int_L F\cdot d\beta. \]
Ideia da demonstração. Neste caso $u(a)=d$ e $u(b)=c$... Fim da ideia da demonstração.
É possível enunciar análogos dos resultados anteriores para caminhos fechados simples seccionalmente $C^1$ que descrevem a mesma linha no mesmo sentido ou em sentidos opostos e adicionalmente com independência relativamente ao ponto em que iniciamos e fechamos o caminho. Em vez de fazê-lo sugere-se que considere o seguinte
Exercício. Mostre que dados caminhos $\alpha(\lambda)= ( \cos \lambda, \sen \lambda)$, $\lambda\in [0,2\pi]$ e $\beta(t)= ( -\sen t^2, -\cos t^2)$, $t\in [0,\sqrt{2\pi}]$ e um campo contínuo $F:\mathbb{R}^2\to \mathbb{R}^2$ temos \[\oint_{S^1}F\cdot d\alpha = \oint_{S^1}F\cdot d\beta.\]
Campos conservativos
Uma questão bem mais importante que as invarâncias relativamente a parametrizações de uma mesma linha é a possível invariância de um integral de linha quando se muda a linha mas mantendo os extremos da mesma. O conceito motivador em Mecânica é o de campo conservativo que passamos a precisar.
Definição (Campo conservativo). Um campo vectorial contínuo $F:A\subset\mathbb{R}^n\to \mathbb{R}^n$, com $A$ um aberto conexo, diz-se conservativo se dados quaisquer dois pontos $\boldsymbol{x}_0, \boldsymbol{x}_1\in A$ o integral de linha \[\int_L F\cdot dr\] toma o mesmo valor para qualquer caminho seccionalmente $C^1$ com início em $\boldsymbol{x}_0$ e fim em $\boldsymbol{x}_1$.
Uma observação quase imediata é que uma caracterização equivalente é o integral ao longo de caminhos fechados seccionalmente $C^1$ ser sempre $0$. Para tornar clara esta observação note que dados dois caminhos com o mesmo início e o mesmo fim, invertendo o sentido a um deles e concatenando-os obtemos um caminho fechado e, dado um caminho fechado, podemos reverter este processo para obter dois caminhos com o mesmo início e o mesmo fim.
Outra caracterização equivalente de campo conservativo obtém-se através do conceito de potencial escalar e dos chamados teoremas fundamentais para integrais de linha que generalizam o teorema fundamental do cálculo e a regra de Barrow ao contexto corrente.
Definição (Potencial escalar). Dado um campo vectorial contínuo $F:A\subset\mathbb{R}^n\to \mathbb{R}^n$, em que $A$ é um conjunto aberto, diz-se que $\varphi:A\to \mathbb{R}$ é um potencial escalar de $F$ se $\varphi$ for diferenciável em $A$ com $\nabla \varphi=F$.
Teorema (fundamental do cálculo para integrais de linha). Seja $A\subset\mathbb{R}^n$ um aberto conexo e $F:A\to\mathbb{R}^n$ um campo conservativo. Então existe $\varphi:A\to\mathbb{R}$ tal que $\nabla \varphi=F$.
Demonstração. Fixemos um ponto $\boldsymbol{x}_0\in A$. Um candidato óbvio a $\varphi$ é o valor do integral de linha (trabalho) \[\int_{L[\boldsymbol{x}_0, \boldsymbol{x}]}F\cdot dr\] em que $L[\boldsymbol{x}_0, \boldsymbol{x}]$ é um qualquer caminho seccionalmente $C^1$ com início em $\boldsymbol{x}_0$ e fim em $\boldsymbol{x}$ (se duvidar que um qualquer ponto de $A$ pode ser atingível por um arco seccionalmente $C^1$, considere este exercício anterior).
Para verificar que $\varphi$ satisfaz os nosso requisitos comecemos por considerar uma derivada parcial de $\varphi$. Temos \[\frac{\partial \varphi}{\partial x_i}(\boldsymbol{x}) =\lim_{t\to 0}\frac{\varphi(\boldsymbol{x}+t\boldsymbol{e}_i) - \varphi(\boldsymbol{x})}{t}. \] Como temos independência do caminho no cálculo do integral de linha usado para definir $\phi$ podemos assumir que o caminho usado no cálculo de $\varphi(\boldsymbol{x}+t\boldsymbol{e}_i)$ é o caminho usado para calcular $\varphi(\boldsymbol{x})$ concatenado com o segmento de recta unindo $\boldsymbol{x}$ a $\boldsymbol{x}+t \boldsymbol{e}_i$. Parametrizando este segmento via $\alpha(\lambda)=\boldsymbol{x}+\lambda t \boldsymbol{e}_i$, com $\lambda\in [0,1]$, obtemos \[\varphi(\boldsymbol{x}+t\boldsymbol{e}_i) - \varphi(\boldsymbol{x})=\int_0^1 F(\boldsymbol{x}+\lambda t \boldsymbol{e}_i)\cdot t \boldsymbol{e}_i \, d\lambda\] donde \[\frac{\partial \varphi}{\partial x_i}(\boldsymbol{x}) =\lim_{t\to 0} \int_0^1 F(\boldsymbol{x}+\lambda t \boldsymbol{e}_i)\cdot \boldsymbol{e}_i \, d\lambda\] que, pela continuidade de $F$, é igual a $F_i(\boldsymbol{x})$, a $i$-ésima coordenada do campo $F$ calculada em $\boldsymbol{x}$ o que estabelece que $\nabla \varphi=F$.
Notando que $F$ é continua, os cálculos anteriores estabelecem que $\varphi\in C^1(A)$ e é portanto diferenciável. Fim de demonstração.
Teorema (análogo da regra de Barrow para integrais de linha). Seja $\varphi:A\subset\mathbb{R}^n\to \mathbb{R}$ com $A$ um aberto conexo e $\varphi\in C^1(A)$. Se $r:[a,b]\to A$ for um caminho seccionalmente de classe $C^1$ com $L=r([a,b])$, então \[ \int_L \nabla \varphi\cdot dr =\varphi(r(b))-\varphi(r(a)).\]
Demonstração. \[ \int_L \nabla \varphi\cdot dr =\int_a^b \nabla \varphi(r(t))\cdot r'(t)\, dt = \int_a^b \frac{d}{dt}(\varphi(r(t))\, dt= \varphi(r(b))-\varphi(r(a)).\] Fim de demonstração.
Destes dois resultados segue
Corolário. Um campo vectorial contínuo num aberto de $\mathbb{R^n}$ é conservativo se e só se for um gradiente de um campo escalar $C^1$ nesse aberto.
Exemplo. Voltemos a considerar o campo vectorial $F:\mathbb{R}^2\setminus\{(0,0)\}\to \mathbb{R}^2$ definido por \[F(x,y)=\left(\frac{x}{x^2+y^2}, \frac{y}{x^2+y^2}\right).\] Como \[\begin{align*}\frac{x}{x^2+y^2}&=\frac{\partial}{\partial x}\left( \frac{1}{2}\log(x^2+y^2)\right) \\ \frac{y}{x^2+y^2}&=\frac{\partial}{\partial y} \left(\frac{1}{2}\log(x^2+y^2)\right) \end{align*}\] este campo possui um potencial escalar $\varphi(x,y)=\frac{1}{2}\log(x^2+y^2)$ e portanto é conservativo. Se pretendermos calcular um integral de linha \[\int_L F\cdot d\beta\] em que $\beta$ é um caminho seccionalmente $C^1$ em $\mathbb{R}^2\setminus\{(0,0)\}$ unindo um ponto a uma distância $R_1>0$ de $(0,0)$ a um ponto a uma distância $R_2>0$ de $(0,0)$, podemos afirmar imediatamente que o valor do integral é $\log(R_2/R_1)$.
Exemplo. Voltemos a considerar o campo vectorial $G:\mathbb{R}^2\setminus\{(0,0)\}\to \mathbb{R}^2$ definido por \[G(x,y)=\left(-\frac{y}{x^2+y^2}, \frac{x}{x^2+y^2}\right).\] Como calculámos um integral de linha de $G$ ao longo de um caminho fechado, cujo valor não era $0$, podemos afirmar que este campo não é conservativo e não existe um seu potencial escalar. Fim de exemplo.
Note-se que o único método que temos até ao momento para decidir pela afirmativa que um campo é um gradiente de um potencial envolve primitivar as componentes do campo e ajustar as "constantes" de primitivação (que não são constantes mas funções desconhecidas das restantes variáveis) algo que não é particularmente prático. Exemplificando com o campo \[(x,y,z)\mapsto \left(\frac{yz}{1+x^2y^2z^2}+y, \frac{xz}{1+x^2y^2z^2}+x, \frac{xy}{1+x^2y^2z^2}+z \right)\] temos que, a existir um potencial $\varphi$, terá que verificar \[\begin{align*}\varphi(x,y,z)& =\int \frac{yz}{1+x^2y^2z^2}+y \, dx = \operatorname{arctg}(xyz)+xy+C_1(y,z), \\ \varphi(x,y,z)& = \int \frac{xz}{1+x^2y^2z^2}+x \, dy = \operatorname{arctg}(xyz)+xy+C_2(x,z) \\ \varphi(x,y,z)& = \int \frac{xy}{1+x^2y^2z^2}+z \, dz = \operatorname{arctg}(xyz)+\frac{z^2}{2}+C_3(x,y)\end{align*}\] algo que é satisfeito (a menos de uma constante aditiva) por \[ \varphi(x,y,z) = \operatorname{arctg}(xyz)+xy + \frac{z^2}{2}. \] Fim de exemplo.
A igualdade de derivadas parciais de segunda ordem cruzadas para funções $C^2$ num aberto dá-nos uma condição necessária mais expedita para um campo $C^1$ ser um gradiente.
Definição (campo fechado). Um campo vectorial $F:A\subset\mathbb{R}^n\to\mathbb{R}^n$ com $A$ um aberto e $F\in C^1(A)$ diz-se fechado se em $A$ \[\frac{\partial F_i}{\partial x_j}=\frac{\partial F_j}{\partial x_i}\] para todos os $i,j=1,\dots,n$.
Proposição (gradientes são campos fechados). Seja $ F:A\subset\mathbb{R^n}$, com $ A $ um aberto e $ F\in C^1 (A) $. Se $ F $ é um gradiente então $ F $ é fechado.
Demonstração.Seja $ F=\nabla\varphi $. Temos \[\frac {\partial F_i}{\partial x_j}=\frac {\partial}{\partial x_j}\left(\frac {\partial \varphi}{\partial x_i}\right)=\frac {\partial}{\partial x_i}\left (\frac {\partial \varphi}{\partial x_j}\right)=\frac{\partial F_j}{\partial x_i}.\] Fim de demonstração.
É importante perceber que, por si só, a condição de um campo ser fechado não é suficiente para assegurar que é um gradiente.
Exemplo. Voltemos a considerar o exemplo relativo ao campo $G:\mathbb{R}^2\setminus\{(0,0)\}\to \mathbb{R}^2$ definido por \[G(x,y)=\left(\frac{-y}{x^2+y^2}, \frac{x}{x^2+y^2}\right).\] O campo é $C^\infty$ e temos \[\frac{\partial}{\partial y}\left(\frac{-y}{x^2+y^2}\right)=\frac{y^2-x ^2}{(x^2+y^2)^2} = \frac{\partial}{\partial x}\left(\frac{x}{x^2+y^2}\right). \] pelo que o campo é fechado. No entanto já vimos um integral ao longo de um caminho fechado $C^1$ deste campo que não é $0$ logo o campo não é conservativo e não é um gradiente.
Por outro lado se considerarmos $\psi:\mathbb{R}^2\setminus\{(x,0): x\geq 0\}\to\mathbb{R}^2$ definido por \[\psi(x,y)=\begin{cases}-\operatorname{arctg}(x/y), & \text{ se } y\gt 0, \\ -\operatorname{arctg}(x/y)+\pi , & \text{ se } y\lt 0, \\ \pi, & \text{ se } y=0 \text{ e } x\leq 0,\end{cases}\] verificamos que $\psi$ é um potencial de $G$ em $\mathbb{R}^2\setminus\{(x,0): x\geq 0\}$ (verifique que $\frac{\partial \psi}{\partial y}$ existe e tem os valores correctos sobre o semi-eixo negativo dos $x$s). Isto é, foi possível restringir $G$ a um subconjunto aberto do seu domínio, cuja diferença para o domínio é um conjunto de alguma forma “pequeno”, aonde já a restrição de $G$ é um gradiente de um potencial.
É possível assim afirmar que, por exemplo, \[\oint_C G\cdot dr = 0\] em que $r(t)=(2+\cos t, \operatorname{sen} t)$, com $t\in [0,2\pi]$ e $C=r([0,2\pi])$. Fim de exemplo.
A questão óbvia que se põe após o exemplo anterior é: existem condições adicionais relativamente ao domínio de um campo fechado que permitam concluir que ele é conservativo? Voltaremos a ela mais tarde mas desde já consideramos um resultado simples desse tipo.
Definição (Conjunto em estrela). Dizemos que $E\subset\mathbb{R}^n$ é um conjunto em estrela se existir $\boldsymbol{x}_0\in E$ tal que qualquer ponto $\boldsymbol{x}\in E$ pode ser ligado a $\boldsymbol{x}_0$ por um segmento de recta contido em $E$, isto é para todo o $t\in [0,1]$ e todo o $\boldsymbol{x}\in E$ temos $(1-t)\boldsymbol{x}_0+t\boldsymbol{x}\in E$.
Exemplos. São exemplos de conjuntos em estrela todos os conjuntos convexos e portanto, em particular, bolas e intervalos. Uma estrela no plano também é em estrela, e daí o nome. Que $\mathbb{R}^n\setminus L$, em que $L$ é uma semi-recta, é também um conjunto em estrela exige um pouco mais de reflexão (faça-o!).
Proposição. Seja $E\subset\mathbb{R}^n$ um conjunto aberto em estrela e $F:E\to\mathbb{R}^n$, $F\in C^1(E)$, um campo fechado. Então $F$ é conservativo.
Demonstração. Definimos $\varphi:E\to\mathbb{R}$ via \[\varphi(\boldsymbol{x})=\int_{L(\boldsymbol{x}_0,\boldsymbol{x})} F\cdot dr\] em que $\boldsymbol{x}_0$ é o ponto na definição de conjunto em estrela e $L(\boldsymbol{x}_0,\boldsymbol{x})$ é o segmento de recta unindo $\boldsymbol{x}_0$ a $\boldsymbol{x}$ parametrizado por $r(t)=(1-t)\boldsymbol{x}_0+t\boldsymbol{x}$, $t\in[0,1]$. Temos \[\varphi(\boldsymbol{x})=\int_0^1 F((1-t)\boldsymbol{x}_0+t\boldsymbol{x})\cdot (\boldsymbol{x}-\boldsymbol{x}_0)\, dt,\] donde, usando a regra de Leibniz, obtemos \[\begin{align*}\frac{\partial \varphi}{\partial x_i} &=\int_0^1 \frac{\partial}{\partial x_i}\left(\sum_{j=1}^n F_j((1-t)\boldsymbol{x}_0+t\boldsymbol{x})(x_j-x_{0j})\right)\, dt \\ &= \int_0^1 F_i((1-t)\boldsymbol{x}_0+t\boldsymbol{x}) + \sum_{j=1}^n t \frac{\partial F_j}{\partial x_ i} ((1-t)\boldsymbol{x}_0+t\boldsymbol{x})(x_j-x_{0j}) \, dt \end{align*}\] Usando que o campo $F$ é fechado, a última igualdade dá lugar a \[\frac{\partial \varphi}{\partial x_i} = \int_0^1 F_i((1-t)\boldsymbol{x}_0+t\boldsymbol{x}) + \sum_{j=1}^n t \frac{\partial F_i}{\partial x_j} ((1-t)\boldsymbol{x}_0+t\boldsymbol{x})(x_j-x_{0j}) \, dt \] O teorema de derivação da função composta permite identificar nesta última expressão que \[\sum_{j=1}^n \frac{\partial F_i}{\partial x_j} ((1-t)\boldsymbol{x}_0+t\boldsymbol{x})(x_j-x_{0j}) =\frac{\partial}{\partial t} \left( F_i((1-t)\boldsymbol{x}_0+t\boldsymbol{x})\right)\] donde \[\begin{align*}\frac{\partial \varphi}{\partial x_i} &= \int_0^1 F_i((1-t)\boldsymbol{x}_0+t\boldsymbol{x}) + t \frac{\partial}{\partial t} \left( F_i((1-t)\boldsymbol{x}_0+t\boldsymbol{x})\right)\, dt\\ &= \int_0^1 \frac{\partial}{\partial t} \left(t F_i((1-t)\boldsymbol{x}_0+t\boldsymbol{x})\right)\, dt = F_i(\boldsymbol{x}).\end{align*}\] Fim de demonstração.
Note que este resultado permite estabelecer muito facilmente, sem recorrer a primitivação e ter que lidar com uma descontinuidade, que o campo $G$ já considerado em exemplos anteriores, definido por $\mathbb{R}^2\setminus\{(0,0)\}\ni (x,y)\mapsto G(x,y) =\left(-\frac{y}{x^2+y^2}, \frac{x}{x^2+y^2}\right)$, é conservativo em conjuntos que correspondam a $\mathbb{R}^2$ exceptuando uma semi-recta com origem em $(0,0)$.
Teorema de Green
A regra de Barrow estabelece que, sendo $a\lt b$, e $f:[a,b]\to\mathbb{R}$ de classe $C^1([a,b])$ temos \[\int_a^b f'(x)\, dx = f(b)-f(a).\]
Note que a igualdade envolve um funcional linear que depende dos valores da derivada de $f$ no seu domínio e um funcional linear de $f$ que só envolve valores de $f$ na fronteira do seu domínio. Vamos estar interessados em resultados que têm estas características mas dizem respeito a funções definidas em limitados de $\mathbb{R}^n$ ou de variedades $k$-dimensionais, com certas características. Vão ser obtidos da regra de Barrow e contêm-na como um caso particular. O mais simples é o chamado teorema de Green. Para introduzi-lo comecemos com um cálculo simples.
Exemplo. Sejam $a\lt b$ dois números reais, $h_1, h_2:[a,b]\to\mathbb{R}$ duas funções contínuas verificando $h_1 \leq h_2$ em $[a,b]$, $U=\{(x,y)\in\mathbb{R}^2: x\in [a,b], h_1(x)\leq y\leq h_2(x)\}$ e $P:U\to\mathbb{R}$, $P\in C^1(U)$.
Note que \[\iint_U \frac{\partial P}{\partial y} \, dx\,dy = \int_a^b\left(\int_{h_1(x)}^{h_2(x)} \frac{\partial P}{\partial y} \, dy\right)dx= \int_a^b P(x,h_2(x))-P(x,h_1(x))\, dx.\]
Por outro lado se considerarmos o integral de linha do campo vectorial $(P,0)$ a um caminho fechado $r$ simples e seccionalmente que percorre $\partial U$ no “sentido directo” verficamos que podemos considerar por concatenação \[\oint_{\partial U} (P,0)\cdot dr = \int_{L_1} (P,0) \cdot dr_1 + \int_{L_2} (P,0) \cdot dr_2 - \int_{L_3}(P,0) \cdot dr_3 - \int_{L_4} (P,0) \cdot dr_4\] em que cada cada $L_i$ corresponde a um “lado” da nossa região parametrizado respectivamente por \[\begin{align*}r_1(t) & =(t,h_1(t)), t\in[a,b], \\ r_2(t) & =(b,t), t\in[h_1(b),h_2(b)], \\ r_3(t) & =(t,h_2(t)), t\in[a,b], \\ r_4(t) & =(a,t), t\in[h_1(a),h_2(a)]. \end{align*}\] Facilmente se verifica que os integrais de linha relativos a $L_2$ e $L_4$ são $0$. Além disso, abreviando a notação dos dois restantes para $\int_{L_1} P \, dx$ e $\int_{L_3} P \, dx$ e de forma similar para o integral ao longo de $\partial U$, obtemos \[ \oint_{\partial U} P \, dx = \int_{L_1} P \, dx - \int_{L_3} P \, dx = \int_a^b P(x, h_1(x))\, dx - \int_a^b P(x, h_2(x))\, dx. \]
Portanto estabelecemos que \[ \oint_{\partial U} P \, dx = -\iint_U \frac{\partial P}{\partial y}\, dx\, dy. \] Fim de exemplo.

Designaremos os subconjuntos de $\mathbb{R}^2$ para os quais vale uma descrição como no exemplo como sendo de tipo U.
Exercício. Estabeleça, de forma análoga ao exemplo anterior, que para regiões da forma $V=\{(x,y)\in \mathbb{R}^2: g_1(y)\leq x \leq g_2(y), y\in [c,d]\}$ com $c\lt d$, $g_1, g_2\in C^0([c,d])$ e $g_1(y) \leq g_2(y)$ para todo o $y\in [c,d]$, vale \[ \oint_{\partial V} Q \, dy =\iint_V \frac{\partial Q}{\partial x}\, dx\, dy, \] com $\partial V$ percorrida por um caminho fechado simples seccionalmente $C^1$ no sentido directo, para toda a função $Q:V\to\mathbb{R}$, $Q\in C^1(V)$. Note a ausência de sinal menos na fórmula e explique-a!
Designaremos os subconjuntos de $\mathbb{R}^2$ para os quais vale uma descrição como no exercício como sendo de tipo V.
Agora é imediato que
Teorema (de Green). Seja $A\subset\mathbb{R}^2$ simultaneamente de tipo U e tipo V e $P,Q:A\to\mathbb{R}$ duas funções de classe $C^1$. Então vale \[\iint_A \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \, dx\,dy = \oint_{\partial A} P\, dx+ Q\, dy \] em que o integral de linha é tomado relativamente a um caminho fechado simples seccionalmente $C^1$ que descreve $\partial A$ no “sentido directo” na acepção descrita no exemplo.
Exemplo. (Área calculada via um integral de linha) Considerando $P(x,y)=-\frac{y}{2}$ e $Q(x,y)=\frac{x}{2}$ (existem outras possibilidades) verificamos que podemos calcular a área de certas regiões do plano através de um integral de linha. Fim de exemplo.
Exemplo. Verificamos facilmente que uma bola é simultaneamente de tipo U e tipo V. Tal já não acontece para $B_2(0,0)\setminus B_ 1(0,0)$. No entanto podemos decompor este último conjunto numa união de dois conjuntos que são simultaneamente de tipo U e de tipo V, aplicar o teorema a cada um deles e adicionar membro a membro as igualdades obtidas com resultados interessantes.

Assim, no caso em que $P, Q: \overline{B_2(0,0)}\setminus B_1(0,0)\to \mathbb{R}$ são funções de classe $C^1$, obtemos \[\oint_{\partial B_2(0,0)}P\, dx + Q\, dy - \oint_{\partial B_1(0,0)}P\, dx + Q\, dy = \iint_{B_2(0,0)\setminus B_1(0,0)} \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \, dx\, dy.\] em que nos integrais de linha convencionamos percorrer a linha em ambos os casos no “sentido directo”. Note cuidadosamente como os integrais de linha nos dois segmentos horizontais se cancelam mutuamente e os sentidos em que se percorrem as circunferências. Fim de exemplo.
Última edição desta versão: João Palhoto Matos, 08/06/2020 13:44:05.