Teorema da função inversa

Dada uma aplicação linear \(A:\mathbb{R}^n\to \mathbb{R}^n\) a condição do determinante da matriz que a representa ser não nulo é equivalente a \(A\) ser uma bijecção. Em que medida é que uma condição similar relativa ao determinante da matriz jacobiana tem reflexos no facto de podermos definir uma inversa de uma função de classe \(C^1\) de \(\mathbb{R}^n\) em \(\mathbb{R}^n\)? Vamos ver que a resposta é em geral negativa mas, se nos contentarmos com uma invertibilidade local de \(F\) a resposta é afirmativa. Tal é o conteúdo do teorema da função da inversa.

Se \(g:\mathbb{R}\to \mathbb{R}\) é uma função de classe \(C^1\) para a qual \(g'(t)\neq 0\) para todo o \(t\in\mathbb{R}\) então podemos concluir que \(g\) é uma função estritamente monótona em \(\mathbb{R}\). Este facto poderia levantar expectativas que se revelam infundadas para funções \(F:\mathbb{R}^n\to\mathbb{R}^n\) verificando \(F\in C^1(\mathbb{R}^n)\) e \(\det J_F(\boldsymbol{x})\neq 0\) para todo o \(\boldsymbol{x}\in \mathbb{R}^n\).

Exemplo. Seja \(F:\mathbb{R}^2\to \mathbb{R}^2\) definida por \(F(x,y)=(e^x\cos y, e^x\operatorname{sen} y)\)

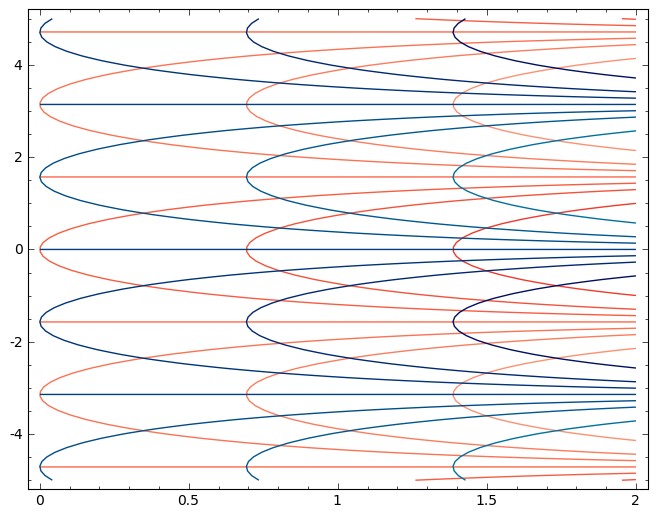
Temos \(F(x,y+2\pi) =F(x,y)\) para todos os \((x,y)\in\mathbb{R}^2\) pelo que a função não é injectiva. No entanto \[J_F(x,y)=\begin{bmatrix}e^x\cos y & -e^x\operatorname{sen} y \\ e^x\operatorname{sen} y & e^x\cos y\end{bmatrix}\]e \(\det J_F(x,y)=e^{2x}\gt 0\). Note-se no entanto que a restrição de \(F\) a uma "faixa horizontal" \(\{(x,y)\in\mathbb{R}^2: \alpha \lt y\lt \alpha + 2\pi\}\) é uma função injectiva. Fim de exemplo.

O teorema da função inversa vai simplesmente garantir que se o determinante da matriz jacobiana de uma aplicação \(C^1\) definida numa aberto de \(\mathbb{R}^n\) com valores em \(\mathbb{R}^n\) é não nulo num dado ponto, então existe uma vizinhança do ponto onde a aplicação é injectiva e a inversa dessa função é também de classe \(C^1\).

Uma possível estratégia de demonstração do teorema baseia-se em considerar uma linearização da equação \(F(\boldsymbol{x})=\boldsymbol{y}\) perto do ponto onde a matriz jacobiana é não nula e mostrar sucessivamente que essa linearização permite construir, desde que comecemos suficientemente perto do ponto, uma sucessão que converge para uma solução da equação e que essa solução é uma função de classe \(C^1\) de \(\boldsymbol{y}\).

Supomos então que \(A\subset\mathbb{R}^n\) é um aberto, \(F:A\to \mathbb{R}^n\) é uma função de classe \(C^1(A)\), \(\boldsymbol{x}_0\in A\) e \(\det J_F(\boldsymbol{x}_0)\neq 0\). Designamos \(\boldsymbol{y}_0=F(\boldsymbol{x}_0)\).

O nosso objectivo é mostrar que existem abertos $V\ni \boldsymbol{y}_0$ e $U\ni \boldsymbol{x}_0$ tais que $F$ é uma bijecção de $U$ sobre $V$ e que $G=(F|_U)^{-1}$ é uma função diferenciável. Note-se que, se esse objectivo for atingido, o teorema de derivação da função composta garante imediatamente que $DG(F(\boldsymbol{x}))DF(\boldsymbol{x})=D(G\circ F)(\boldsymbol{x})=I$, com $I$ a aplicação linear identidade, para todo o $\boldsymbol{x}\in U$, o que nos permite relacionar as derivadas de $F$ e $G$ e, atendendo ao que sabemos do processo de cálculo da matriz inversa, justifica que $G\in C^1(V)$.

Substituímos temporariamente a consideração da equação \(F(\boldsymbol{x})=\boldsymbol{y}\) para \(\boldsymbol{x}\) “perto” de \(\boldsymbol{x}_0\) e \(\boldsymbol{y}\) “perto” de \(\boldsymbol{y}_0\) pela consideração da equação linearizada \[F(\boldsymbol{x}_0)+DF(\boldsymbol{x}_0)(\boldsymbol{x}-\boldsymbol{x}_0)=\boldsymbol{y}\] cuja solução é \[\boldsymbol{x}= \boldsymbol{x}_0 + DF(\boldsymbol{x}_0)^{-1}(\boldsymbol{y}-F(\boldsymbol{x}_0)).\]

A igualdade anterior pode ser interpretada como calculando, a partir de uma primeira aproximação à solução de \(F(\boldsymbol{x})=\boldsymbol{y}\), uma nova aproximação através de um operador \(T_{\boldsymbol{y}}\) definido por \[T_{\boldsymbol{y}}(\boldsymbol{x})=\boldsymbol{x} + DF(\boldsymbol{x}_0)^{-1}(\boldsymbol{y}-F(\boldsymbol{x})).\]

Toda a ideia da demonstração consiste em provar que, se recursivamente voltarmos a repetir este processo, construímos uma sucessão convergente para uma solução da equação original, desde que tenhamos considerado \(\boldsymbol{y}\) suficientemente perto de \( \boldsymbol{y}_0=F(\boldsymbol{x}_0)\). Esta ideia para solução de equações não lineares é conhecida por método de Newton, frequentemente utilizado para cálculo numérico.

Consideramos então \(\boldsymbol{y}\in B_\epsilon(\boldsymbol{y}_0)\), com $\epsilon\gt 0$ a ser restringido posteriormente, e definimos uma sucessão recursivamente via \[\boldsymbol{x}_{k+1}=T_{\boldsymbol{y}}(\boldsymbol{x}_k), \text{ para } k\in\mathbb{N}.\]

Como \[\boldsymbol{x}_{k+1}=\boldsymbol{x}_{k+1} - \boldsymbol{x}_k + \boldsymbol{x}_k = \boldsymbol{x}_{k+1} - \boldsymbol{x}_k + \boldsymbol{x}_k - \boldsymbol{x}_{k-1} + \boldsymbol{x}_{k-1}=\dots =\sum_{j=1}^k ( \boldsymbol{x}_{j+1} - \boldsymbol{x}_j) + \boldsymbol{x}_0, \] provar a convergência da sucessão é equivalente a provar a convergência da série telescópica \[\sum_{j=0}^{+\infty}(\boldsymbol{x}_{j+1}-\boldsymbol{x}_{j}),\] sendo o limite da sucessão igual a \(\boldsymbol{x}_0\) mais a soma da série.

Por sua vez, para provar a convergência da série $\sum (\boldsymbol{x}_{j+1}-\boldsymbol{x}_{j})$, mostramos que a série das normas dos seus termos pode ter o seu termo geral majorado por o de uma série geométrica de razão menor que $1$, desde que que tenhamos a garantia de que todos os $\boldsymbol{x}_{j}$ estão numa bola $B_r(\boldsymbol{x}_0)$ com raio \(r\gt 0\) suficientemente pequeno.

Que a convergência da série das normas implica a convergência de uma série de termos em \(\mathbb{R}^n\), tem uma demonstração análoga à demonstração do teorema sobre convergência absoluta de séries numéricas.

Sejam \(\boldsymbol{x},\boldsymbol{z}\in B_r(\boldsymbol{x}_0)\subset A\). Então \[T_{\boldsymbol{y}}(\boldsymbol{x})-T_{\boldsymbol{y}}(\boldsymbol{z})=\boldsymbol{x}-\boldsymbol{z}-DF(\boldsymbol{x}_0)^{-1}(F(\boldsymbol{x})-F(\boldsymbol{z}))\] o que sugere considerar a função \(\boldsymbol{x}\mapsto \boldsymbol{x}-DF(\boldsymbol{x}_0)^{-1}F(\boldsymbol{x})\equiv H(\boldsymbol{x})\) para aplicação do teorema de Lagrange para funções vectoriais. A derivada desta função é \(DH(\boldsymbol{x})=I-DF(\boldsymbol{x}_0)^{-1}DF(\boldsymbol{x})\) em que \(I\) designa a aplicação linear identidade. Note-se que todas as derivadas parciais na matriz jacobiana de \(H\), tendem para \(0\) quando \(\boldsymbol{x}\to\boldsymbol{x}_0\). Assim, dado um qualquer \(\alpha\) com \(1\gt \alpha\gt 0\), é possível escolher \(\delta\), com $0\lt \delta\lt r$, tal que para \(\boldsymbol{x}, \boldsymbol{z}\in B_\delta(\boldsymbol{x}_0)\) temos \[\begin{equation}\|T_{\boldsymbol{y}}(\boldsymbol{x})-T_{\boldsymbol{y}}(\boldsymbol{z})\|\leq \alpha\|\boldsymbol{x}-\boldsymbol{z}\|\label{eq:contracao}\end{equation}\] donde \[\|\boldsymbol{x}_{k+1}-\boldsymbol{x}_k\|\leq \alpha \|\boldsymbol{x}_{k}-\boldsymbol{x}_{k-1}\| \leq\dots\leq \alpha^k\|\boldsymbol{x}_{1}-\boldsymbol{x}_0\|\] desde que tenhamos a garantia de que cada \(\boldsymbol{x}_k\) está na bola \(B_\delta(\boldsymbol{x}_0)\).

Para justificarmos que os termos da sucessão $(\boldsymbol{x}_k)$ não se afastam de mais de $\boldsymbol{x}_0$ estimamos, para $\boldsymbol{x}\in B_\delta(\boldsymbol{x}_0)$ e $\boldsymbol{y}\in B_\epsilon(\boldsymbol{y}_0)$, \begin{align*}\|T_{\boldsymbol{y}}(\boldsymbol{x})-\boldsymbol{x}_0\| & =\|T_{\boldsymbol{y}}(\boldsymbol{x})-T_{\boldsymbol{y}}(\boldsymbol{x}_0)+T_{\boldsymbol{y}}(\boldsymbol{x}_0)-\boldsymbol{x}_0\|\\ & \leq \alpha \|\boldsymbol{x}-\boldsymbol{x}_0\| + \| DF(\boldsymbol{x}_0)^{-1}(\boldsymbol{y}-\boldsymbol{y}_0)\| \\ & \leq \alpha \delta + M \epsilon\end{align*} para alguma constante $M\gt 0$ tal que $\|DF(\boldsymbol{x}_0)^{-1}\boldsymbol{u}\|\leq M\|\boldsymbol{u}\|$ para qualquer $\boldsymbol{u}\in\mathbb{R}^n$ (relembre a discussão da continuidade das aplicações lineares).

Portanto, se $\epsilon\lt  (1-\alpha)/M$, temos $\|T_{\boldsymbol{y}}(\boldsymbol{x})-\boldsymbol{x}_0\|\lt \delta$, ou seja $T_{\boldsymbol{y}}(\boldsymbol{x})\in B_\delta(\boldsymbol{x}_0)$, o que nos garante que a convergência da sucessão de aproximações está garantida se $\delta$ e $\epsilon$ forem escolhidos suficientemente pequenos.

Seja \(\boldsymbol{x}^\ast\in B_{\delta}(\boldsymbol{x}_0)\) o limite da sucessão $(\boldsymbol{x}_k)$. Note-se que, como depende de $\boldsymbol{y}\in B_\epsilon(\boldsymbol{y}_0)$, será conveniente designarmo-lo por \(G(\boldsymbol{y})\) sempre que necessário.

Passando ao limite na igualdade \(T_y(\boldsymbol{x}_k)=\boldsymbol{x}_{k+1}\), usando a continuidade de $T_{\boldsymbol{y}}$ como função de $\boldsymbol{x}$, obtemos que \(\boldsymbol{x}^\ast\) é uma solução de \(T_y(\boldsymbol{x})=\boldsymbol{x}\) e portanto de \(F(\boldsymbol{x})=\boldsymbol{y}\). Estabeleceu-se portanto a existência de solução local da equação \(F(\boldsymbol{x})=\boldsymbol{y}\) na forma $\boldsymbol{x}=G(\boldsymbol{y})$.

Exemplo. Considere-se \(F:\{(x,y)\in\mathbb{R}^2: x+y\gt 0\}\to \mathbb{R}^2\) definida por \[F(x,y)=(e^{x}+\log(x+y), x+y+y^2).\] Trata-se de uma função de classe \(C^1\) no seu domí­nio, sendo a respectiva matriz jacobiana \[J_F(x,y)=\begin{bmatrix}e^{x}+\frac{1}{x+y} & \frac{1}{x+y} \\ 1 & 1+2y \end{bmatrix}\] e, em particular, \[J_F(0,1)=\begin{bmatrix}2 & 1 \\ 1 & 3 \end{bmatrix}\] donde \(\det(J_F(0,1))=5\gt 0\). Daí que existam abertos \(U, V\) com \((0,1)\in U\) e \(F(0,1)=(0,2)\in V\) tais que \(F\) é uma bijecção de \(U\) sobre \(V\) com inversa \(G\in C^1(V)\) verificando \[J_G(0,2)= \begin{bmatrix}2 & 1 \\ 1 & 3 \end{bmatrix}^{-1}=\frac{1}{5}\begin{bmatrix}3 & -1 \\ -1 & 2 \end{bmatrix}.\]