Noções topológicas

Introduzem-se noções topológicas elementares para subconjuntos de \(\mathbb{R}^n\), alguns exemplos e caracterizam-se os fechados usando sucessões.

Definição (ponto interior, interior). Dados um conjunto \(A\subset\mathbb{R}^n\) e \(\boldsymbol{x}\in\mathbb{R}^n\), diz-se que \(\boldsymbol{x}\) é interior a \(A\) se existir uma bola \(B_r(\boldsymbol{x})\subset A\). O conjunto de todos os pontos interiores de um dado conjunto designa-se como o seu interior, abreviadamente \(\operatorname{int} A\).

De notar que que todos os pontos interiores pertencem necessariamente ao conjunto e que portanto \(\operatorname{int} A\subset A\).

Definição (Conjunto aberto). Se um conjunto for igual ao seu interior diz-se aberto.

Exemplo. Considere-se $B=\{(x,y)\in\mathbb{R}^2:y \gt x^2\}$. Trata-se de um conjunto aberto como facilmente nos convencemos considerando um ponto \((x_0,y_0)\) tal que \(y_0 \gt x_0^2\). Tal ponto está a uma distância positiva da parábola \(y=x^2\), embora estimar o valor de \(r\gt 0\) tal que \[B_r(x_0,y_0)\subset B\] não seja imediato (veremos que há uma maneira prática de justificar a afirmação mais à frente).

Se considerarmos o conjunto \[S=\{(x,y)\in\mathbb{R}^2:y\geq x^2\} \] é fácil justificar que não é aberto pois, para todos os pontos da parábola \(y=x^2\) e bolas centradas neles, encontramos em tais bolas tanto pontos que pertencem a \(S\) como pontos que não pertencem a \(S\). A pontos com esta propriedade damos o nome de pontos fronteiros. Fim de exemplo.

Definição (ponto aderente, fecho). Dados um conjunto \(F\subset\mathbb{R}^n\) e \(\boldsymbol{x}\in\mathbb{R}^n\) diz-se que \(\boldsymbol{x}\) é um ponto aderente a \(F\) se for um ponto fronteiro ou um ponto de \(F\). A \(F\cup\partial F\) chamamos fecho de \(F\), que abreviamos \(\overline{F}\).

Definição (Conjunto fechado). Um subconjunto de $\mathbb{R}^n$ que é igual ao seu fecho diz-se fechado.

Relembramos também que

Definição (ponto fronteiro, fronteira). Dados um conjunto \(A\subset\mathbb{R}^n\) e \(\boldsymbol{x}\in\mathbb{R}^n\) diz-se que \(\boldsymbol{x}\) é um ponto fronteiro de \(A\), ou simplesmente fronteiro a \(A\), se qualquer que seja a bola \(B_r(\boldsymbol{x})\) esta contenha tanto pontos de \(A\) como do seu complementar. Ao conjunto de todos os pontos fronteiros chamamos fronteira, abreviadamente \(\partial A\).

Ocasionalmente será conveniente distinguir dois tipos de pontos aderentes: os pontos isolados e os pontos de acumulação.

Definição (ponto de acumulação, derivado). Dados um conjunto \(F\subset\mathbb{R}^n\) e \(\boldsymbol{x}\in\mathbb{R}^n\) diz-se que \(\boldsymbol{x}\) é um ponto de acumulação de \(F\) se qualquer que seja a bola $B_r(\boldsymbol{x})$ esta contém um ponto de $F$ distinto de $\boldsymbol{x}$.

Exercício. Mostre que \(\boldsymbol{x}\) é um ponto de acumulação de $F$ se e só se dada uma qualquer bola $B_r(\boldsymbol{x})$ nesta existir um número infinito de pontos de $F$.

Definição (ponto isolado). Dados um conjunto \(F\subset\mathbb{R}^n\) e \(\boldsymbol{x}\in\mathbb{R}^n\) diz-se que \(\boldsymbol{x}\) é um ponto isolado de \(F\) se existir uma bola $B_r(\boldsymbol{x})$ tal que $F\cap B_r(\boldsymbol{x})=\{\boldsymbol{x}\}$.

Definição (ponto exterior, exterior). Dados um conjunto \(S\subset\mathbb{R}^n\) e \(\boldsymbol{x}\in\mathbb{R}^n\) diz-se que \(\boldsymbol{x}\) é um ponto exterior a \(S\) se for um ponto interior ao complementar de $S$. Ao conjunto de pontos exteriores chama-se exterior de $S$, $\operatorname{ext} S$.

Exercício. Justifique que $\operatorname{ext} S=\mathbb{R}^n\setminus \overline{S}$.

Convém verificar que a nossa utilização das palavras aberto e fechado, no que toca a subconjuntos de \(\mathbb{R}^n\) em geral e de bolas em particular, é coerente. De facto

Proposição. Uma bola aberta é um conjunto aberto.

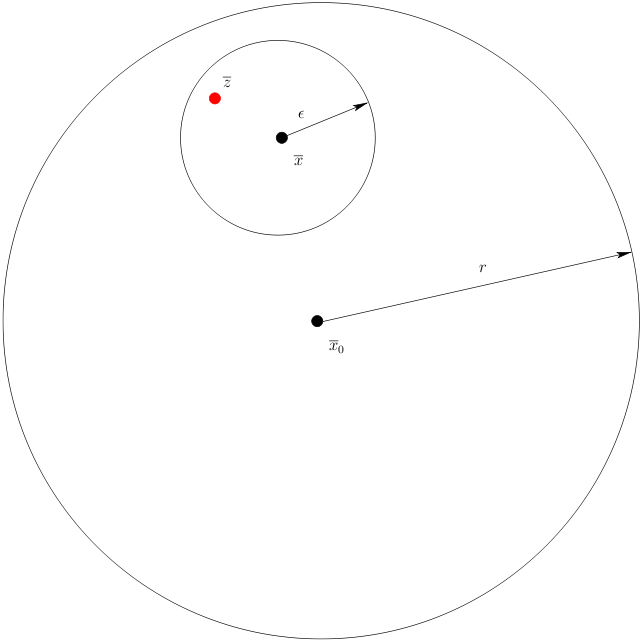
Demonstração: O que precisamos de fazer é mostrar que, dada uma bola aberta \(B_r(\boldsymbol{x}_0)\) e um ponto \(\boldsymbol{x}\in B_r(\boldsymbol{x}_0)\), existe um valor de \(\epsilon \gt 0\) tal que \(B_\epsilon(\boldsymbol{x})\subset B_r(\boldsymbol{x}_0)\), ou, o que é o mesmo, que conseguimos escolher \(\epsilon \gt 0\) tal que dado um qualquer \(\boldsymbol{z}\in B_\epsilon(\boldsymbol{x})\) então \(\|\boldsymbol{z}-\boldsymbol{x}\| \lt r\).

Estimando a distância de \(\boldsymbol{z}\) a \(\boldsymbol{x}_0\) via a desigualdade triangular obtemos \[\|\boldsymbol{z}-\boldsymbol{x}_0\|=\|\boldsymbol{z}-\boldsymbol{x}+\boldsymbol{x}-\boldsymbol{x}_0\|\leq \|\boldsymbol{z}-\boldsymbol{x}\| + \|\boldsymbol{x}-\boldsymbol{x}_0\|\lt \epsilon + \|\boldsymbol{x}-\boldsymbol{x}_0\|.\] Como \(\|\boldsymbol{x}-\boldsymbol{x}_0\|\lt r\) podemos escolher $\epsilon$ de maneira a $0 \lt \epsilon \lt r - \|\boldsymbol{x}-\boldsymbol{x}_0\|$. Fim de demonstração.

Exercício. Verifique também que uma bola fechada é um conjunto fechado (isto é ainda mais simples do que a proposição anterior).

Note que exterior, fronteira e interior de um conjunto são conjuntos disjuntos dois a dois e tais que a sua união é \(\mathbb{R}^n\).

Proposição. O complementar de um conjunto aberto é fechado.

Ideia da demonstração: Seja \(A\) um conjunto aberto. Queremos provar que \(\mathbb{R}^n\setminus A\) é fechado, ou seja que \(\mathbb{R}^n\setminus A\) contém a sua fronteira \(\partial(\mathbb{R}^n\setminus A)\). Verifique que a fronteira de um conjunto e do seu complementar coincidem. Fim da ideia de demonstração.

Proposição. O complementar de um conjunto fechado é aberto.

Ideia da demonstração: Seja \(F\) um conjunto fechado. Queremos provar que \(\mathbb{R}^n\setminus F\) é aberto, ou seja que qualquer um dos seus pontos é interior. Isto é óbvio pois tal ponto não pertencendo ao fecho de \(F\) é centro de uma bola que não contém pontos de \(F\). Fim da ideia de demonstração.

Exercício. Verifique que tanto \(\mathbb{R}^n\) como \(\emptyset\) são conjuntos simultaneamente abertos e fechados.

Exercício. Verifique que não existe um conjunto distinto de \(\mathbb{R}^n\) e \(\emptyset\) simultaneamente aberto e fechado. [Sugestão: Supondo que tal conjunto existia considere um segmento de recta unindo um ponto no conjunto a um ponto no complementar do conjunto. Mostre que existe um ponto neste segmento de recta que pertence à intersecção das aderências do conjunto e do seu complementar.]

Exercício. Mostre que uma união de conjuntos abertos é um conjunto aberto. Mostre que uma intersecção de um número finito de conjuntos abertos é um conjunto aberto.

Exercício. Mostre que uma união de um numero finito de conjuntos fechados é um conjunto fechado. Mostre que uma intersecção de conjuntos fechados é um conjunto fechado.

Exercicio. Mostre que o conjunto $\cup_{k=1}^{+\infty}\;{\left]k,k+\frac{1}{k}\right[}$ é um conjunto aberto.

Exercício. Dê um exemplo de uma intersecção de conjuntos abertos que não é um conjunto aberto.

Exercício. Seja \(S=\mathbb{Q}\cap[0,1]\). Determine \(\operatorname{int} S\), \(\operatorname{ext} S\), \(\partial S\).

Um tema recorrente relativo a noções topológicas é a utilização de sucessões para caracterizá-las. É o que vamos fazer com a noção de conjunto fechado.

Proposição (caracterização de fechados via sucessões). Um conjunto \(F\subset\mathbb{R}^n\) é fechado sse dada uma qualquer sucessão convergente de termos em \(F\) o seu limite é também um elemento de \(F\).

Demonstração. Seja \(F\subset\mathbb{R}^n\) fechado e \((\boldsymbol{x}_k)\) uma sucessão de termos em \(F\) convergente para \(\boldsymbol{x}^\ast\). Dada uma qualquer bola centrada em \(\boldsymbol{x}^\ast\) segue da definição de limite que existe uma ordem a partir da qual todos os termos da sucessão estão nessa bola. Mas isso quer dizer que \(\boldsymbol{x}^\ast\in\overline{F}=F\) visto \(F\) ser fechado.

Reciprocamente suponha-se que \(F\) não era fechado. Então existia \(\boldsymbol{x}_\ast\in \overline{F}\setminus F\). Daí que para cada \(k\in\mathbb{N}\) podemos escolher \(\boldsymbol{x}_k\in F\cap B_{1/k}(\boldsymbol{x}_\ast)\). Mas então \(\boldsymbol{x}_k\to \boldsymbol{x}_\ast\) fornecendo um exemplo de uma sucessão de termos em \(F\) convergindo para um ponto que não pertence a \(F\). Fim da demonstração.

Juntamente com a caracterização dos limitados via sucessões, tal permite obter

Teorema (caracterização dos limitados e fechados via sucessões). \(S\subset \mathbb{R}^n\) é limitado e fechado se e só se dada uma qualquer sucessão de termos em \(S\) esta possuir uma subsucessão convergente para um ponto do conjunto.

Note que as nossas definições acima de limitado e fechado são coerentes com o uso destas palavras na definição de intervalo limitado e fechado já usada quando definimos integral.

Como última observação sobre este tópico fazemos notar que

Definição (vizinhança de um ponto). Vizinhança de um ponto é um qualquer aberto contendo o ponto.

Isto contrasta com a utilização da mesma palavra quando lidámos com funções reais de variável real.