Definição (derivada parcial). Seja \(F:A\subset\mathbb{R}^n\to\mathbb{R}^m\) e \(\boldsymbol{x}_0\in A\). Dizemos que \(F\) possui derivada parcial em ordem à variável $x_j$ no ponto $\boldsymbol{x}_0$, \(\frac{\partial F}{\partial x_j}(\boldsymbol{x}_0)\), se existir (e for finito) o limite \[\lim_{\lambda\to 0} \frac{F(\boldsymbol{x}_0+\lambda \boldsymbol{e}_j)-F(\boldsymbol{x}_0)}{\lambda}.\] onde \(\boldsymbol{e}_j\) designa o \(j\)-ésimo vector da base canónica de \(\mathbb{R}^n\), isto é um vector cuja \(j\)-ésima coordenada é \(1\) e as restantes \(0\). Nesse caso a derivada parcial fica definida como o valor do limite.

Tal é equivalente a calcular o vector cujas coordenadas são as derivadas de cada uma das funções reais de variável real \[\lambda \mapsto F_i(x_{01},\dots,x_{0j-1},\lambda,x_{0j+1},\dots,x_{0n})\] com \(i=1,\dots,m\) e \(j=1,\dots,n\), em que $F=(F_i)_{i=1,\dots,m}$, o que torna o cálculo de derivadas parciais redutí­vel ao cálculo de derivadas como já as conhecíamos.

Exemplo. Seja $f:\mathbb R^2\to\mathbb R$ definida por $f(x,y)=e^{x^2y}+\cos(xy^2)$. O cálculo das derivadas parciais de $f$ corresponde a considerar uma das variáveis como a variável e a outra como constante. \begin{align*}\frac{\partial f}{\partial x}&=2xy e^{x^2y} - y^2 \sen(xy^2) \\ \frac{\partial f}{\partial y}&=x^2 e^{x^2y} - 2xy \sen(xy^2)\end{align*}

Fim de exemplo.

Exemplo. Seja $g:\mathbb R^2\to\mathbb R$ definida por \[g(x,y)=\begin{cases} \frac{y^3}{x^2+y^2} &\text{ se } (x,y)\neq (0,0) \\ 0, & \text{ se } (x,y)= (0,0)\end{cases}\] Então \begin{align*}\frac{\partial g}{\partial y}(0,0) &=\lim_{\lambda\to 0} \frac{g(0,\lambda) - g(0,0)}{\lambda} \\ &=\lim_{\lambda \to 0} \frac{\lambda^3}{\lambda^2 \lambda}=1\end{align*} ou mais simplesmente notando que $g(0,y)=y$ para todo o $y$ e que a derivada desta função de $y$ é $1$.

Fim de exemplo.

Este conceito de derivada parcial peca por não garantir as propriedades que já nos habituámos a esperar da diferenciabilidade.

Considere-se \(H:\mathbb{R}^2\to\mathbb{R}\) definida por \[H(x,y)=\begin{cases}0, & \text{ se } x\neq 0 \text{ e } y\neq 0, \\ 1, & \text{ se } x= 0 \text{ ou } y=0.\end{cases}\] \(H\) não é contínua em \((0,0)\) e possui ambas as derivadas parciais nulas em \((0,0)\). Portanto a existência de derivadas parciais num ponto não garante a continuidade nesse ponto.

Definição (derivada segundo um vector, derivada dirigida, derivada direccional). Seja \(F:A\subset\mathbb{R}^n\to\mathbb{R}^m\), \(\boldsymbol{x}_0\in A\) e \(\boldsymbol{v}\in\mathbb{R}^n\setminus\{\boldsymbol{0}\}\). Dizemos que \(F\) possui derivada dirigida ou segundo o vector \(\boldsymbol{v}\) em \(\boldsymbol{x}_0\), \(D_{\boldsymbol{v}}(\boldsymbol{x}_0)\), se existir o limite \[\lim_{\lambda\to 0}\frac{F(\boldsymbol{x}_0+\lambda \boldsymbol{v}) - F(\boldsymbol{x}_0)}{\lambda}.\] Nesse caso a derivada dirigida fica definida como o valor do limite. Se o vector for unitário falamos de derivada direccional.

Alterando a geometria do exemplo anterior obtemos um exemplo simples de uma função que possui num ponto todas as derivadas dirigidas mas não é contínua. De facto seja \(G:\mathbb{R}^2\to\mathbb{R}\) definida por \[G(x,y)=\begin{cases}1, & \text{ se } y=x^2 \text{ e } (x,y)\neq (0,0), \\ 0, & \text{ caso contrário.}\end{cases}\]

Se considerarmos \((0,0)\) e qualquer \(\boldsymbol{v}\in\mathbb{R}^n\), a razão incremental de que necessitamos de calcular o limite só é não nula no máximo num único ponto (correspondente à intersecção da recta definida por \((0,0)\) e \(\boldsymbol{v}\) com a parábola \(y=x^2\)) e consequentemente \(D_\boldsymbol{v}G(0,0)=0\) para todo o \(\boldsymbol{v}\). No entanto \(G\) não é contínua em \((0,0)\) pois em qualquer bola centrada em \((0,0)\) existem pontos onde \(G\) vale \(1\) e outros onde vale \(0\).

Podemos inclusivamente dar um exemplo de uma função \(F:\mathbb{R}^2\to \mathbb{R}\) contínua em \(\mathbb{R}^2\setminus\{(0,0)\}\), não contínua em \((0,0)\) e que possui todas as derivadas dirigidas em \((0,0)\), recorrendo a um exemplo já conhecido. Seja então\[F(x,y)=\begin{cases}\frac{x y^2}{x^2+y^4}, & \text{ se } (x,y)\neq (0,0), \\ 0, & \text{ caso contrário.}\end{cases}\] Já vimos que \(F\) não é contínua em \((0,0)\) (recorrendo, por exemplo, aos valores de \(F\) sobre as parábolas \(x=\pm y^2\)). Se \((u,v)\neq (0,0)\) consideremos então\begin{align*}D_{(u,v)}F(0,0) &=\lim_{\lambda\to 0}\frac{F(\lambda u, \lambda v)}{\lambda}\\ & =\lim_{\lambda\to 0}\frac{\lambda^3 u v^2}{\lambda(\lambda^2 u^2+\lambda^4 v^4)}\\ & =\begin{cases}\frac{v^2}{u}, & \text{ se } u\neq 0, \\ 0, & \text{ se } u= 0.\end{cases}\end{align*}

Definição (Diferenciabilidade). Seja \(F:S\subset\mathbb{R}^n\to \mathbb{R}^m\) e \(\boldsymbol{x}\in \operatorname{int} S\). Dizemos que \(F\) é diferenciável em \(\boldsymbol{x}\) se existir uma aplicação linear \(T:\mathbb{R}^n\to \mathbb{R}^m\) tal que\[\lim_{\boldsymbol{h}\to 0}\frac{F(\boldsymbol{x}+\boldsymbol{h})-F(\boldsymbol{x})-T(\boldsymbol{h})}{\|\boldsymbol{h}\|}= \boldsymbol{0}.\]

Note que:

• Só discutimos diferenciabilidade em pontos interiores ao domínio de uma função.
• No caso de \(m=n=1\), funções reais de variável real, a condição na definição equivale à existência de derivada finita num ponto interior ao domínio. (Verifique, relembrando que as aplicações lineares de \(\mathbb{R}\) em \(\mathbb{R}\) são os produtos por números reais).

Proposição (Diferenciabilidade das constantes). As funções constantes num aberto são diferenciáveis tendo como derivada a aplicação linear nula.

Demonstração. Podemos considerar \(T\) como a aplicação linear nula. Fim de demonstração.

Proposição (Diferenciabilidade das aplicações lineares). As aplicações lineares são diferenciáveis tendo como derivada a mesma aplicação linear.

Demonstração. Podemos considerar \(T\) como sendo a própria função. Fim de demonstração.

Proposição. A aplicação linear \(T\) na definição de diferenciabilidade se existir é única.

Demonstração. Suponhamos que duas aplicações lineares distintas \(T_1\) e \(T_2\) satisfaziam a condição na definição de diferenciabilidade. Há-de existir algum vector \(\boldsymbol{u}\in \mathbb{R}^n\) tal que \(T_1(\boldsymbol{u})\neq T_2(\boldsymbol{u})\). Mas devemos ter, por restrição do domí­nio ao tomarmos o limite, \[\lim_{\lambda\to 0}\frac{F(\boldsymbol{x}+\lambda\boldsymbol{u})-F(\boldsymbol{x})-T_1(\lambda\boldsymbol{u})}{\|\lambda\boldsymbol{u}\|}=\lim_{\lambda\to 0}\frac{F(\boldsymbol{x}+\lambda\boldsymbol{u})-F(\boldsymbol{x})-T_2(\lambda\boldsymbol{u})}{\|\lambda\boldsymbol{u}\|}=\boldsymbol{0}\] Mas então também\[\lim_{\lambda\to 0}\frac{\lambda(T_1(\boldsymbol{u})-T_2(\boldsymbol{u}))}{|\lambda|\|\boldsymbol{u}\|}=\boldsymbol{0}\] uma condição que contradiz \(T_1(\boldsymbol{u})\neq T_2(\boldsymbol{u})\). Fim da demonstração.

Definição (Derivada (total)). À transformação linear única na definição de diferenciabilidade chamamos derivada (total) de \(F\) em \(\boldsymbol{x}\), abreviadamente \(DF(\boldsymbol{x})\).

Assim a derivada duma função constante num aberto é a aplicação linear nula em qualquer ponto desse aberto e a derivada de uma aplicação linear é constante e igual à própria aplicação linear.

Note-se que \(F\) é diferenciável em \(\boldsymbol{x}\) com derivada \(DF(\boldsymbol{x})\) se e só se existir uma função \(\mathcal{E}_F(\boldsymbol{x},\boldsymbol{h})\) tal que \[\begin{cases} F(\boldsymbol{x}+\boldsymbol{h})=F(\boldsymbol{x})+DF(\boldsymbol{x})(\boldsymbol{h}) +\mathcal{E}_F(\boldsymbol{x},\boldsymbol{h}), \\  \displaystyle \lim_{\boldsymbol{h}\to\boldsymbol{0}}\frac{\mathcal{E}_F(\boldsymbol{x},\boldsymbol{h})}{\|\boldsymbol{h}\|}=\boldsymbol{0}. \end{cases}\]

Tal permite-nos obter

Proposição (Diferenciabilidade implica continuidade). Se \(F\) (como na definição de diferenciabilidade) for diferenciável num ponto então \(F\) é contínua nesse ponto.

Proposição (Diferenciabilidade das funções vectoriais). \(F=(F_i)_{i=1,\dots, m}\) como na definição de diferenciabilidade é diferenciável num ponto se e só se cada uma das suas funções coordenadas \(F_i\) for diferenciável nesse ponto.

Proposição (Diferenciabilidade e derivadas dirigidas). Se \(F\) como na definição de diferenciabilidade for diferenciável num ponto \(\boldsymbol{x}\) então existem todas as derivadas dirigidas de \(F\) em \(\boldsymbol{x}\) com\[D_vF(\boldsymbol{x})=DF(\boldsymbol{x})(\boldsymbol{v}).\]

Proposição (Diferenciabilidade e matriz jacobiana). Se \(F\) como na definição de diferenciabilidade for diferenciável num ponto \(\boldsymbol{x}\) então \(DF(\boldsymbol{x})\) actua sobre vectores de \(\mathbb{R}^n\) via \[DF(\boldsymbol{x})(\boldsymbol{h})=J_F(\boldsymbol{x})(\boldsymbol{h})\] em que \(J_F(\boldsymbol{x})=\left[\frac{\partial F_i}{\partial x_j}(\boldsymbol{x})\right]_{i=1,\dots,m, j=1,\dots, n}\) é a matriz jacobiana de \(F\) no ponto \(\boldsymbol{x}\).

Os vectores linha da matriz jacobiana, \(\nabla F_i(\boldsymbol{x})=\left(\frac{\partial F_i}{\partial x_j}\right)_{j=1,\dots,n}\), designam-se por vectores gradiente das coordenadas de \(F\).  Os vectores coluna, \(\frac{\partial F}{\partial x_j}=\left(\frac{\partial F_i}{\partial x_j}\right)_{i=1,\dots,m}\), correspondem às derivadas parciais de \(F\) relativamente a cada uma das variáveis.

Exemplo (Diferenciabilidade do produto). Consideremos a aplicação \(\mathbb{R}^2\ni(x,y)\mapsto xy =f(x,y)\). Pretendemos estudar a sua diferenciabilidade num ponto qualquer de \(\mathbb{R}^2\). Dado que\[\begin{align*}\frac{\partial f}{\partial x} & =y, \\ \frac{\partial f}{\partial y} & =x \end{align*}\] a matriz jacobiana de \(f\) é \[J_f(x,y)=\begin{bmatrix}y & x\end{bmatrix}\] A ser \(f\) diferenciável a derivada de \(f\) actuará sobre vectores de \(\mathbb{R}^2\) via \[\mathbb{R}^2\ni(h,k)\mapsto y h+x k =\nabla f(x,y)\cdot (h,k).\]

Para estudar a diferenciabilidade é então necessário considerar o limite \[\begin{gather*}\lim_{(h,k)\to(0,0)}\frac{f(x+h,y+k)-f(x,y)-\nabla f(x,y)\cdot(h,k)}{\sqrt{h^2+k^2}}\\ =\lim_{(h,k)\to(0,0)}\frac{x y+y h+k x+h k-x y-y h-k x}{\sqrt{h^2+k^2}} =\lim_{(h,k)\to(0,0)}\frac{h k}{\sqrt{h^2+k^2}}=0.\end{gather*}\] Portanto \(f\) é diferenciável em qualquer ponto de \(\mathbb{R}^2\).

Exemplo (Significado do gradiente). Para uma função escalar diferenciável o gradiente é um vector com um significado em termos de direcção e norma muito especial. Se \(f\) for uma tal função, \(\boldsymbol{x}\) um ponto onde a função é diferenciável e \(\boldsymbol{u}\) um vector unitário de \(\mathbb{R}^n\) temos \[D_{\boldsymbol{u}}f(\boldsymbol{x})=\nabla f(\boldsymbol{x})\cdot \boldsymbol{u}.\] Recordando a desigualdade de Cauchy-Schwarz e as condições a que se reduz uma igualdade temos, se $\nabla f(\boldsymbol{x})\neq \boldsymbol{0}$, \[\sup_{\|\boldsymbol{u}\|=1} D_{\boldsymbol{u}}f(\boldsymbol{x}) = \|\nabla f(\boldsymbol{x})\| = D_{\frac{\nabla f(\boldsymbol{x})}{\|\nabla f(\boldsymbol{x})\|}}f(\boldsymbol{x}). \] Daí que o gradiente tenha a direcção e sentido da maior "taxa de crescimento" em valor absoluto da função escalar e o valor da sua norma é essa "taxa de crescimento".

Teorema (Derivação da função composta). Sejam \(F:A\subset\mathbb{R}^n\to \mathbb{R}^m\) e \(G:B\subset\mathbb{R}^m\to \mathbb{R}^p\) funções tais que \(F\) é diferenciável num ponto \(\boldsymbol{x}_0\in \operatorname{int}A\) e \(G\) é diferenciável em \(F(\boldsymbol{x}_0)\in \operatorname{int}B\). Então \(G\circ F\) é diferenciável em \(\boldsymbol{x}_0\) verificando-se \[D(G\circ F)(\boldsymbol{x}_0)=DG(F(\boldsymbol{x}_0))DF(\boldsymbol{x}_0).\]

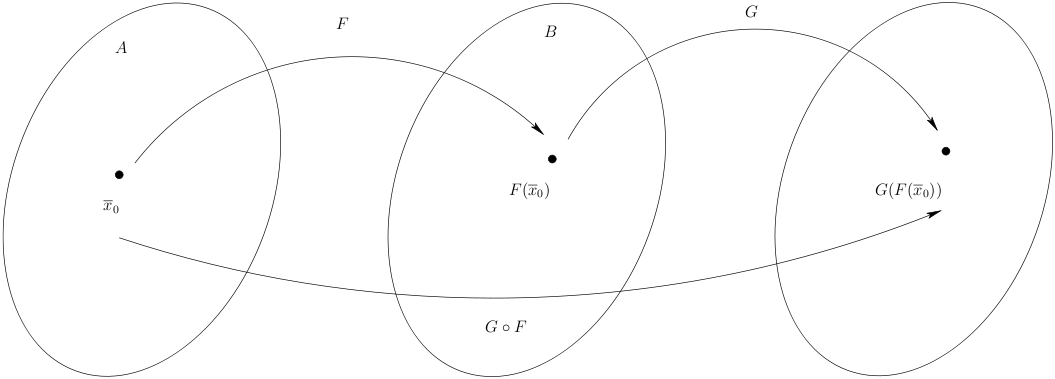
Demonstração. Comecemos por verificar que \(\boldsymbol{x}_0\) é um ponto interior do domínio de \(G\circ F\). O domínio de \(G\circ F\) é o conjunto dos pontos de \(A\) cuja imagem por \(F\) pertence a \(B\). Considere-se uma bola \(B_\epsilon(F(\boldsymbol{x}_0))\subset B\) (algo possí­vel por \(F(\boldsymbol{x}_0)\in \operatorname{int}B\)). Como \(F\) é diferenciável também é contínua e portanto existirá uma bola \(B_\delta(\boldsymbol{x}_0)\) tal que se \(\boldsymbol{x}\in B_\delta(\boldsymbol{x}_0) \cap A\) também \(F(\boldsymbol{x})\in B_\epsilon(F(\boldsymbol{x}_0))\). Como \(\boldsymbol{x}_0\in \operatorname{int}A\) existe outra bola \(B_\gamma(\boldsymbol{x}_0)\subset A\). Então, tomando \(\alpha=\min(\delta,\gamma)\), \(B_\alpha(\boldsymbol{x}_0)\subset A\) e a imagem de todos os seus pontos está em \(B\) concluindo que \(\boldsymbol{x}_0\) é um ponto interior do domínio de \(G\circ F\).

Passemos propriamente à verificação da diferenciabilidade de \(G\circ F\) em \(\boldsymbol{x}_0\). Seja \(\boldsymbol{h}\in\mathbb{R}^n\), \(\|\boldsymbol{h}\|<\alpha\). Convencionamos escrever \(\boldsymbol{v}=F(\boldsymbol{x}_0+\boldsymbol{h})-F(\boldsymbol{x}_0)\). Então \begin{align*}& G(F(\boldsymbol{x}_0+\boldsymbol{h}))-G(F(\boldsymbol{x}_0)) \\ \qquad & =  DG(F(\boldsymbol{x}_0))(\boldsymbol{v})+\mathcal{E}_G(F(\boldsymbol{x}_0);\boldsymbol{v}) \\  \qquad & = DG(F(\boldsymbol{x}_0))(DF(\boldsymbol{x}_0)(\boldsymbol{h})+\mathcal{E}_F(\boldsymbol{x}_0;\boldsymbol{h}))+\mathcal{E}_G(F(\boldsymbol{x}_0);\boldsymbol{v}) \\  \qquad & =  DG(F(\boldsymbol{x}_0))DF(\boldsymbol{x}_0)(\boldsymbol{h})+DG(F(\boldsymbol{x}_0))(\mathcal{E}_F(\boldsymbol{x}_0;\boldsymbol{h}))+\mathcal{E}_G(F(\boldsymbol{x}_0);\boldsymbol{v}).\end{align*}

Para concluir a demonstração bastará mostrar que tanto \[ \begin{equation}\lim_{\boldsymbol{h}\to \boldsymbol{0}} \frac{DG(F(\boldsymbol{x}_0))(\mathcal{E}_F(\boldsymbol{x}_0;\boldsymbol{h}))}{\|\boldsymbol{h}\|}=\boldsymbol{0} \label{eq:1}\end{equation}\] como \[\begin{equation}\lim_{\boldsymbol{h}\to\boldsymbol{0}}\frac{\mathcal{E}_G(F(\boldsymbol{x}_0);\boldsymbol{v})}{\|\boldsymbol{h}\|}=\boldsymbol{0}.\label{eq:2}\end{equation}\]

Fim da demonstração.

Em termos de matrizes jacobianas a relação entre derivadas traduz-se em \[J_{G\circ F}(\boldsymbol{x}_0) = J_G(F(\boldsymbol{x}_0))J_F(\boldsymbol{x}_0).\]

Em termos de elementos das matrizes jacobianas, convencionando variáveis dependentes via $\boldsymbol{u}=(u_i)_{i=1,\dots,p}=G(F(\boldsymbol{x}))$,  $\boldsymbol{y}=(y_k)_{k=1,\dots,m}= F(\boldsymbol{x})$, $\boldsymbol{x}=(x_j)_{j=1,\dots,n}$ obtemos \[ \frac{\partial u_i}{\partial x_j}(\boldsymbol{x}_0)=\sum_{k=1}^n \frac{\partial u_i}{\partial y_k}(F(\boldsymbol{x}_0))\frac{\partial y_k}{\partial x_j}(\boldsymbol{x}_0)\] uma fórmula que é conhecida como regra da cadeia devido ao seu aspecto tipográfico.

Diferenciabilidade do produto, quociente,...

Vamos usar o teorema de derivação da função composta e resultados conhecidos para garantir a diferenciabilidade e calcular a derivada do produto de duas funções escalares diferenciáveis.

Sejam \(f,g:S\subset\mathbb{R}^n\to \mathbb{R}\) duas funções diferenciáveis num ponto \(\boldsymbol{x}\in S\) e seja \(h:S\subset\mathbb{R}^n\to \mathbb{R}\) definida por \(h(\boldsymbol{x})=f(\boldsymbol{x})g(\boldsymbol{x})\). Notamos que \(h=p\circ \psi\) em que \(\psi:S\to\mathbb{R}^2\) é definida por \(\psi(\boldsymbol{x})=(f(\boldsymbol{x}), g(\boldsymbol{x}))\) e \(p:\mathbb{R}^2\to\mathbb{R}\) é definida por \(p(u,v)=uv\). Temos que \(\psi\) é diferenciável pois cada uma das suas funções coordenadas é diferenciável e podemos justificar que \(p\) com os cálculos já usados num exemplo anterior. O teorema de derivação da função composta garante a diferenciabilidade de \(h\). Notamos que \[J_\psi(\boldsymbol{x}) = \begin{bmatrix}\nabla f(\boldsymbol{x}) \\ \nabla g(\boldsymbol{x}) \end{bmatrix}\] e \[J_p(u,v)= \begin{bmatrix} v & u \end{bmatrix}\] pelo que \[J_h(\boldsymbol{x})=J_p(\psi(\boldsymbol{x})) J_\psi(\boldsymbol{x}) = \begin{bmatrix} g(\boldsymbol{x}) & f(\boldsymbol{x}) \end{bmatrix}\begin{bmatrix}\nabla f(\boldsymbol{x}) \\ \nabla g(\boldsymbol{x}) \end{bmatrix} =\begin{bmatrix}g(\boldsymbol{x}) \nabla f (\boldsymbol{x}) + f(\boldsymbol{x}) \nabla g (\boldsymbol{x})\end{bmatrix} \] o que constitui uma generalização da regra de derivação do produto que abreviaremos \(\nabla(fg)=g\nabla f + f\nabla g\).

Exemplo. Muitas vezes usaremos o teorema de derivação da função composta para relacionar as derivadas parciais de duas funções.

Seja \(F:\mathbb{R}^2\to \mathbb{R}\) diferenciável em \(\mathbb{R}^2\) e definimos \(G:\mathbb{R}^2\to \mathbb{R}\) via \[G(x,y)=F(xy, x^2-y^2).\] O teorema de derivação da função composta juntamente com a diferenciabilidade de polinómios garante a diferenciabilidade de \(G\) e \[J_G(x,y)=J_F(xy, x^2-y^2)\begin{bmatrix}y & x \\ 2x & -2y\end{bmatrix}\] pelo que \[\begin{align*}\frac{\partial G}{\partial x} & =  y\; D_1F(xy, x^2-y^2)  + 2x\; D_2F(xy, x^2-y^2)  \\ \frac{\partial G}{\partial y} & =  x\; D_1F(xy, x^2-y^2) - 2y\; D_2F(xy, x^2-y^2) \end{align*}\]

Exemplo. Considere-se a aplicação \(T:\mathbb{R}^3\to\mathbb{R}^3\) que transforma coordenadas esféricas em coordenadas cartesianas, via \[T(\rho,\theta,\phi)=(\rho\cos \theta \operatorname{sen}\phi,\rho\operatorname{sen} \theta \operatorname{sen}\phi,\rho\cos\phi).\] Note-se que a aplicação como descrita não é injectiva e é usual restringir tanto quanto possí­vel o domí­nio de maneira ao conjunto em que a injectividade falha ser "pequeno" mas mantendo sobrejectividade. Uma restrição possí­vel comum é considerar \((\rho,\theta,\phi)\in {[0,+\infty[}\times{[0,2\pi[}\times{[0,\pi]}\). Dessa forma a função ainda não é injectiva visto, por exemplo, \(T(0,\theta,\phi)=(0,0,0)\) para todos os \((\theta,\phi)\).

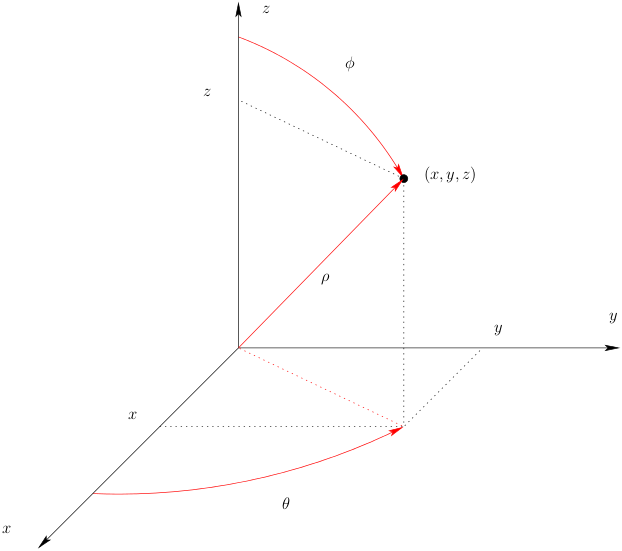
Se uma grandeza for descrita em coordenadas cartesianas por uma uma função \(F:A\subset\mathbb{R}^3\to \mathbb{R}\), a mesma grandeza será descrita em coordenadas esféricas por \(F\circ T\), ou seja por \((\rho,\theta,\phi)\mapsto G(\rho,\theta,\phi)=F\circ T (\rho,\theta,\phi)=F(\rho\cos \theta \operatorname{sen}\phi,\rho\operatorname{sen} \theta \operatorname{sen}\phi,\rho\cos\phi)\). Supondo \(A\) aberto e \(F\) diferenciável também \(G\) será diferenciável e \[DG(\rho,\theta,\phi)=DF(T(\rho,\theta,\phi))DT(\rho,\theta,\phi)\] que explicitada nos permite obter relações entre as derivadas parciais de \(G\) e \(F\) tais como \[\frac{\partial G}{\partial \rho}= \cos\theta \operatorname{sen}\phi \frac{\partial F}{\partial x}+ \operatorname{sen}\theta \operatorname{sen}\phi \frac{\partial F}{\partial y} + \cos\phi  \frac{\partial F}{\partial z}\]

Exemplo. Considere uma função \(F:A\subset\mathbb{R}^n\to B\subset\mathbb{R}^n\) com \(A\) aberto uma bijecção diferenciável cuja inversa, \(F^{-1}\), também é diferenciável (o facto da inversa ser diferenciável não é um dado adquirido, como mostra a função \(x\mapsto x^3\)) para $x=0$. Então \(F^{-1}\circ F(\boldsymbol{x})=\boldsymbol{x}\) para todo o \(\boldsymbol{x}\in A\). Diferenciando esta igualdade obtemos \[DF^{-1}(F(\boldsymbol{x}))DF(\boldsymbol{x})=I\] em que \(I\) designa a aplicação linear identidade. Daí­ que \[DF^{-1}(F(\boldsymbol{x}))=DF(\boldsymbol{x})^{-1}.\] Em particular, nestas condições, a derivada de \(F\) é não singular, sendo portanto o determinante da respectiva matriz jacobiana não nulo. Voltaremos a estas questões e cálculos quando discutirmos o teorema da função inversa.

Exemplo. Seja \(f:A\subset\mathbb{R}^n\to \mathbb{R}\) uma função diferenciável e \(c\in \mathbb{R}\) um valor no seu contradomínio. Consideremos o conjunto de nível de \(f\) relativamente ao valor \(c\), \[N_f(c)=\{\boldsymbol{x}\in A: f(\boldsymbol{x})=c\}.\] Seja \(\boldsymbol{r}:{]0,1[}\to N_f(c)\) uma função diferenciável. À função \(\boldsymbol{r}\) chamaremos um caminho no conjunto de nível \(N_f(c)\). A derivada de \(\boldsymbol{r}\), que abreviaremos \(\boldsymbol{r}'\), pode ser identificada com um vector em \(\mathbb{R}^n\). Este vector terá uma direcção tangente a \(N_f(c)\). Notamos que \[f(\boldsymbol{r}(t))=c\] para todo o \(t\in {]0,1[}\) pelo que, usando o teorema de derivação da função composta, \[\nabla f(\boldsymbol{r}(t))\cdot \boldsymbol{r}'(t)=0\] para todo o \(t\in {]0,1[}\). Interpretamos esta igualdade como estabelecendo a ortogonalidade entre o gradiente e os conjuntos de nível da função. Voltaremos a este assunto quando estudarmos o espaço tangente e o espaço normal a uma variedade e problemas de extremos condicionados.

Exemplo. Seja $f:\mathbb{R}^2\to\mathbb{R}$ definida por \[f(x,y)=\begin{cases}\frac{x^2y^2}{x^2+y^2}, & \text{ se } (x,y)\neq (0,0),\\ 0, & \text{ se } (x,y)= (0,0).\end{cases}\] No complementar da origem é fácil estabelecer a diferenciabilidade da função. No entanto, em $(0,0)$ o único método ao nosso dispor é usar a definição de diferenciabilidade. Como a função é identicamente nula sobre os eixos coordenados temos $\frac{\partial f}{\partial x}(0,0)=\frac{\partial f}{\partial y}(0,0)=0$. Portanto, a ser $f$ diferenciável em $(0,0)$, a sua derivada aí será a aplicação linear nula. Assim estudar a diferenciabilidade em $(0,0)$ corresponde a estudar o limite \[\lim_{(x,y)\to (0,0)} \frac{f(x,y)-f(0,0)-x\frac{\partial f}{\partial x}(0,0) - y\frac{\partial f}{\partial y}(0,0)}{(x^2+y^2)^{1/2}}=\lim_{(x,y)\to (0,0)}\frac{x^2y^2}{(x^2+y^2)^{3/2}}.\] Que o limite existe e vale $0$ decorre da estimativa \[0 \leq \frac{x^2y^2}{(x^2+y^2)^{3/2}}\leq \frac{(x^2+y^2)^2}{(x^2+y^2)^{3/2}}=\sqrt{x^2+y^2}.\] Portanto $f$ é também diferenciável em $(0,0)$ tendo nesse ponto derivada nula.