Soluções

Ficha 11 — Teoremas de Green e da divergência

Tente resolver os exercícios seguintes tanto quanto possível tirando partido dos teoremas de Green ou da divergência:

1. Calcule \[\oint_L -\frac{y}{x^2+y^2}\, dx +\frac{x}{x^2+y^2} \, dy\] em que $L$ é a linha descrita pelo caminho $r(t)=(2\cos t, \operatorname{sen} t)$, $t\in [0,2\pi]$.
2. Seja $A\subset\mathbb{R}^2$ um aberto limitado simplesmente conexo e com fronteira seccionalmente $C^1$. Sejam $u, v: A\to\mathbb{R}^2$ duas funções de classe $C^2(\overline{A})$. Exprima o integral de linha \[\oint_{\partial A}\left(v\frac{\partial u}{\partial x}- u \frac{\partial v}{\partial x}\right)dx +\left(u\frac{\partial v}{\partial y}- v \frac{\partial u}{\partial y}\right)\, dy, \] em que $\partial A$ é suposta percorrida uma vez no “sentido directo”, em termos de um integral duplo apropriado envolvendo $u$, $v$ e as suas derivadas parciais até à segunda ordem.
   Solução

   Com $P(x,y)=v\frac{\partial u}{\partial x}- u \frac{\partial v}{\partial x}$ e $Q(x,y)=u\frac{\partial v}{\partial y}- v \frac{\partial u}{\partial y}$, pelo Teorema de Green sabemos que \[\oint_{\partial A}P\, dx +Q \, dy = \iint_A \left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y} \right) \, dx\, dy.\] Ora, \[\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}=\frac{\partial u}{\partial x}\frac{\partial v}{\partial y}+u\frac{\partial^2  v}{\partial x \partial y}-\frac{\partial u}{\partial y}\frac{\partial v}{\partial x}-v\frac{\partial^2  u}{\partial x \partial y}-\frac{\partial u}{\partial x}\frac{\partial v}{\partial y}-v\frac{\partial^2  u}{\partial y \partial x}+\frac{\partial u}{\partial y}\frac{\partial v}{\partial x}+u\frac{\partial^2  v}{\partial y \partial x}.      \] Uma vez que $u$ e $v$ são funções de classe $C^2(A)$, \[\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}=2\left(u\frac{\partial^2  v}{\partial x \partial y}-v\frac{\partial^2  u}{\partial x \partial y}\right)\] e \[\oint_{\partial A}\left(v\frac{\partial u}{\partial x}- u \frac{\partial v}{\partial x}\right)dx +\left(u\frac{\partial v}{\partial y}- v \frac{\partial u}{\partial y}\right)\, dy=2 \iint_A\left(u\frac{\partial^2  v}{\partial x \partial y}-v\frac{\partial^2  u}{\partial x \partial y}\right)\, dx\, dy.\]

3. Calcule o fluxo do campo $\mathbb{R}^3\ni(x, y, z) \mapsto \psi(x, y, z) = (x^2 , y^2 , z^2 −2xz −2yz)$ através da fronteira da região $R =\left \{(x, y, z) ∈ \mathbb{R}^3 : x^2 +y^2 +z^2 \leq 1 , z \geq 0 , x \geq 0 , y \geq 0\right\}$ no sentido da respectiva normal exterior.
4. Calcule \[\iint_{\partial D}F\cdot\nu \, dS \] em que \[D=\{(x,y,z)\in\mathbb{R}^3:x > 0, y>0, z>0, x+y+z<1\},\] $\nu$ é a respectiva normal unitária exterior e $F(x,y,z)=(x+e^{y^2+z^2},y+e^{z^2+x^2},z+e^{x^2+y^2} )$.
   Solução

   Dado que $\div F=3$ o teorema da divergência permite obter \begin{align*}\iint_{\partial D} F\cdot \nu\, dS & = \iiint_D \div F \, dx\, dy\, dz \\ &= \int_0^1\left(\int_0^{1-x}\left(\int_0^{1-x-y}3\, dz\right) dy\right)dx \\ & = 3\int_0^1\left(\int_0^{1-x} 1-x-y\; dy\right)dx \\ &= 3 \int_0^1 (1-x)^2 - \frac{(1-x)^2}{2}\, dx = \frac{1}{2}. \end{align*}

Volte a considerar, desta vez usando o teorema da divergência:

5. Calcule o fluxo do campo $F:\mathbb{R}^3\to \mathbb{R}^3$ definido por $F(x,y,z)=(x, -2x+y, z)$ através da superfície $\left\{(x, y, z)\in\mathbb{R}^3 : x+2y+z=1, x\geq 0, y\geq 0, z\geq 0\right\}$ com sentido da normal unitária com terceira componente positiva.
6. Calcule o fluxo do campo $G :\mathbb{R}^3\to \mathbb{R}^3$ definido por $G(x, y, z) = (yz, xz, xy)$ através da superfície definida por $\left\{(x, y, z)\in\mathbb{R}^3 : x^2 + y^2 + z^2 = 1, z\gt 0\right\}$ com sentido da normal unitária com terceira componente positiva.
   Solução

   Para utilizarmos o Teorema da Divergência, é natural considerar a região \[D=\left\{(x, y, z)\in\mathbb{R}^3 : x^2 + y^2 + z^2 \leq 1, z\geq 0\right\},\] com fronteira $\partial D=A \cup B$ onde \[A=\left\{(x, y, z)\in\mathbb{R}^3 : x^2 + y^2 + z^2 = 1, z\gt 0\right\}\] e \[B=\left\{(x, y, 0)\in\mathbb{R}^3 : x^2 + y^2 \leq 1\right\}.\] Vem então \[\iint_A G \cdot \boldsymbol{n_e}\,dS +\iint_B  G\cdot \boldsymbol{n_e}\,dS=\iiint_D  \div G\,dx\,dy\,dz,\] em que $ \boldsymbol{n_e}$ designa a normal unitária exterior (que, em todo o ponto de $A$, tem terceira componente positiva). Mas, em $B$, tem-se $ \boldsymbol{n_e}=-e_3$, logo  $G \cdot \boldsymbol{n_e}=-xy$ e, consequentemente, \[\iint_B  G\cdot \boldsymbol{n_e}\,dS=-\iint_{B_1(0,0)}xy\, dx\, dy =-\int_0^{2\pi}\left(\int_0^1 r^3 \cos \theta\operatorname{sen}\theta \, dr\right)d\theta=0.\] Por outro lado, $\div G=0$ e, portanto, \[\iiint_D  \div G\,dx\,dy\,dz=0.\] Concluímos assim que $\iint_A G \cdot \boldsymbol{n_e}\,dS=0$.

   Veja também a solução em que o fluxo é calculado directamente.
7. Seja $H:\mathbb{R}^3\to \mathbb{R}^3$ definido por \[H(x,y,z)=(x+\sen(yz), y+ \cos(xz), z^3+\arctg(xy)).\] Calcule \[\iint_{\partial B_1(0,0,0)}H\cdot \nu\, dS,\] em que $\nu$ é a normal unitária exterior a $B_1(0,0,0)$.
8. Para $r\gt 0$ define-se \[g(r)=\iint_{\partial B_r(0,0,0)}F\cdot \nu\, dS \] em que $F(x,y,z)=(x^2, -2xy+e^{y^3+3x^2y}, z)$ e $\nu$ é a normal unitária exterior a $B_r(0,0,0)$. Calcule, ou mostre que não existe, $\lim_{r\to +\infty} g(r)$.
   Solução

   Pelo teorema da divergência \begin{align*}g(r) & =\iiint_{B_r(0,0,0)} \operatorname{div} F \, dx\, dy\, dz \\ & = \iiint_{B_r(0,0,0)} 3(x^2+y^2) e^{y^3+3x^2y} +1 \, dx\, dy\, dz \\ & \geq \iiint_{B_r(0,0,0)} 1 \, dx\, dy\, dz = \frac{4\pi r^3}{3}\to +\infty\end{align*} pelo que $\lim_{r\to + \infty} g(r)=+\infty$.

9. Seja $h$ uma função definida em $\mathbb{R}^2$ com valores reais não negativos e de classe $C^1$.

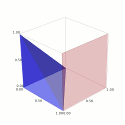
   Considere a região $U$ definida por \[ U = \{(x,y,z)\in\mathbb{R}^3:0\leq z\leq h(x,y), x^2+y^2 \leq 1 \}, \] a superfície $S$ definida por \[ S = \{(x,y,z)\in\mathbb{R}^3:z= h(x,y), x^2+y^2 \leq 1 \}, \] e o campo vectorial $G:U\to\mathbb{R}^3$ definido por \[G(x,y,z)=(-xy ,x^2, yz).\]

   Aplique o teorema da divergência a $G$ em $U$ para mostrar que o fluxo $\iint_S G\cdot \nu \, dS$, com $\nu$ uma normal unitária contínua sobre $S$ num sentido por si arbitrado, não depende de $h$.

   Solução

   Pelo teorema da divergência \begin{equation}\iint_S G\cdot \nu \, dS = \iiint_U \div G \, dx\, dy\, dz - \iint_{S_l} G\cdot \nu \, dS - \iint_{S_0} G\cdot \nu \, dS \label{eq:1}\end{equation} em que \begin{align*}S_l & = \{(x,y,z)\in\mathbb{R}^3: x^2+y^2= 1 , 0\leq z\leq h(x,y)\}, \\ S_0 & = \{(x,y,z)\in\mathbb{R}^3: x^2+y^2\leq 1, z=0\},\end{align*} $\nu$ tem terceira coordenada positiva sobre $S$, $\nu = (x,y,0)$ sobre $S_l$ e $\nu=(0,0,-1)$ sobre $S_0$.

   O integral triplo do lado direito de ($\ref{eq:1}$) é $0$ pois $\div G=0$.

   O fluxo de $G$ através de $S_l$ no lado direito de ($\ref{eq:1}$) é $0$ pois, em $S_l$, $G\cdot \nu = (-xy ,x^2, yz) \cdot (x,y,0)=0$. Analogamente em $S_0$, pois $G\cdot \nu = (-xy ,x^2, 0) \cdot (0,0,-1)=0$.

   Portanto $\iint_S G\cdot \nu \, dS=0$.

10. Mostre que, se $G:\mathbb{R}^3\setminus\{(0,0,0)\}\to \mathbb{R}^3$ é um campo de classe $C^1(\mathbb{R}^3\setminus\{(0,0,0)\})$ tal que \begin{gather*} \lim_{(x,y,z)\to (0,0,0)} (x^2+y^2+z^2)\|G(x,y,z)\|=0,\\ \div G= 0 \text{ em $\mathbb{R}^3\setminus\{(0,0,0)\}$,}\end{gather*} então, sendo $\nu$ a normal unitária exterior a $B_1(0,0,0)$, \[\iint_{\partial B_1(0,0,0)} G\cdot \nu \, dS=0.\]
    Solução

    Usando o teorema da divergência para a função $G$ no domínio $B_1(0,0,0)\setminus B_\epsilon(0,0,0)$ com $0\lt \epsilon\lt 1$ obtemos \begin{equation}0=\iiint_{B_1(0,0,0)\setminus B_\epsilon(0,0,0)}\div G \, dx\,dy\, dz= \iint_{\partial B_1(0,0,0)}G\cdot\nu \, dS - \iint_{\partial B_\epsilon(0,0,0)}G\cdot \boldsymbol{n} \, dS \label{eq2_6_T2B_201819}\end{equation} em que $\boldsymbol{n}$ é a normal unitária exterior a $B_\epsilon(0,0,0)$.

    Ora, usando que $G$ é contínua no limitado e fechado $\partial B_\epsilon(0,0,0)$, temos \begin{equation}\left|\iint_{\partial B_\epsilon(0,0,0)}G\cdot \boldsymbol{n} \, dS\right|\leq \iint_{\partial B_\epsilon(0,0,0)} \|G\| \,dS \leq \max_{\partial B_\epsilon(0,0,0)}\|G\| 4\pi \epsilon^2. \label{eq3_6_T2B_201819}\end{equation} Como $\lim_{(x,y,z)\to (0,0,0)} (x^2+y^2+z^2)\|G(x,y,z)\|=0$ podemos afirmar que o lado direito de (\ref{eq3_6_T2B_201819}) tende para $0$ e daí que \[\lim_{\epsilon\to 0} \iint_{\partial B_\epsilon(0,0,0)}G\cdot \boldsymbol{n} \, dS = 0.\] Consequentemente, passando ao limite quando $\epsilon\to 0$ em (\ref{eq2_6_T2B_201819}), obtemos que \[\iint_{\partial B_1(0,0,0)} G\cdot \nu \, dS=0.\]