Solução do 2º Teste, versão B, 2016/06/06

1. Considere uma função $\psi:\mathbb{R}^2\to\mathbb{R}^2$ definida por $\psi(x,y)=\left(x-2y+e^{x^2-y^2},x+y\right)$. Mostre que:

   1. Existe um aberto $U$ contendo $(0,0)$ onde $\psi$ é injectiva.
   2. Designando a inversa da restrição de $\psi$ a $U$ por $\phi$, calcule a matriz jacobiana $J_\phi(1,0)$.
   Solução

   1. Como $F\in C^1(\mathbb{R}^2)$, a respectiva matriz jacobiana em $(0,0)$ é \[J_\psi(0,0)=\left.\begin{bmatrix}1+2x e^{x^2-y^2} & -2 -2ye^{x^2-y^2} \\ 1 & 1 \end{bmatrix}\right|_{(x,y)=(0,0)} = \begin{bmatrix} 1 & -2 \\ 1 & 1\end{bmatrix}\] e o respectivo determinante é \[\det J_\psi(0,0) = 3 \neq 0\] podemos invocar o teorema da função inversa para garantir que existe um aberto contendo $(0,0)$ onde $\psi$ é injectiva com uma inversa local de classe $C^1$ definida num aberto contendo $\psi(0,0)=(1,0)$.

   2. Designando essa inversa local por $\phi$ temos \[J_\phi(1,0)= J_\psi(0,0)^{-1} = \begin{bmatrix} 1 & -2 \\ 1 & 1\end{bmatrix}^{-1}= \frac{1}{3} \begin{bmatrix} 1 & 2 \\ -1 & 1\end{bmatrix} \]

2. Calcule, usando coordenadas polares, \[\lim_{\epsilon\to 0}\iint_{A_\epsilon}\frac{1}{(x^2+y^2)^{1/3}}\, dx\, dy\] em que $A_\epsilon=\left\{(x,y)\in\mathbb{R}^2: \epsilon\leq \sqrt{x^2+y^2}\leq 1, 0\leq y\leq x\right\}$ com $\epsilon\gt 0$.

   Solução

   

   Usando coordenadas polares\[\iint_{A_\epsilon}\frac{1}{(x^2+y^2)^{1/3}}\, dx\, dy =\int_0^{\pi/4}\left(\int_\epsilon^1 r^{1-2/3}\, dr\right)d\theta = \frac{\pi}{4} \int_\epsilon^1 r^{1/3}\, dr = \frac{\pi}{4} \frac{3}{4} (1-\epsilon^{4/3}).\] Daí que \[\lim_{\epsilon\to 0}\iint_{A_\epsilon}\frac{1}{(x^2+y^2)^{1/3}}\, dx\, dy = \frac{3\pi}{16}.\]

3. Seja $B=\left\{(x,y)\in\mathbb{R}^2: 0< y\leq x^3 ,\frac{y^3}{2}\leq x\leq y\right\}$ e $f:\mathbb{R}\to\mathbb{R}$ uma função contínua. Aplique a mudança de variável \[ \begin{cases}u=x^3/y \\ v=y^3/x \end{cases}\] para transformar o integral \[\iint_B x y f(x^2 y^2)\,dx\, dy\] num integral de uma função adequada num triângulo em $\mathbb{R}^2$.

   Solução

   

   A aplicação $(x,y)\mapsto (u,v)$ é injectiva e $C^1$ no interior do primeiro quadrante com matriz jacobiana \[\begin{bmatrix}3x^2/y & -x^3/y^2 \\ -y^3/x^2 & 3 y^2 /x\end{bmatrix}\] com determinante $8xy$.

   A região de integração transforma-se no plano $uv$ no triângulo limitado pelas linhas $u=v$, $u=1$ e $v=2$.

   

   Obtemos \[\iint_B x y f(x^2 y^2)\,dx\, dy = \int_{1}^2\left(\int_u^2 \frac{1}{8}f(uv)\, dv\right)du.\]

4. Calcule $\int_L \frac{x\, dx +y \, dy + z\, dz}{x^2+y^2+z^2+1}$ em que $L$ é uma linha descrita por um caminho $C^1$ unindo $(0,1,0)$ a $(1,0,1)$.

   Solução

   Temos $\frac{1}{x^2+y^2+z^2+1}(x,y,z)=\nabla \left(\frac{1}{2}\log(x^2+y^2+z^2+1)\right)$ pelo que, por aplicação da versão da regra de Barrow para integrais de linha, \[\int_L \frac{x\, dx +y \, dy + z\, dz}{x^2+y^2+z^2+1}=\frac{1}{2} (\log 3 - \log 2). \].

5. Decida se o conjunto $V$ definido por \[\begin{cases}z= (x+y)^2+(x-y)^2,\\ z= 1- 4x^2-y^2.\end{cases}\] é ou não uma variedade diferenciável e, na afirmativa, determine a sua dimensão e o respectivo espaço tangente em $\left(\frac{1}{\sqrt{6}},0,\frac{1}{3}\right)$.
   Solução

   Seja $F:\mathbb{R}^3\to \mathbb{R}^2$ definida por $F(x,y,z)=(z- (x+y)^2-(x-y)^2, z- 1+ 4x^2+y^2)$. $V$ é o confunto dos zeros de $V$. $F$ é uma função de classe $C^\infty$ e a respectiva matriz jacobiana é \[J_F(x,y,z)=\begin{bmatrix}-4x & -4y & 1 \\ 8x & 2y & 1 \end{bmatrix}\] Reconhece-se, considerando as submatrizes correspondentes à primeira e terceira colunas e à segunda e terceira coluna, que a não existência de duas colunas linearmente independentes desta matriz obrigaria a $x=y=0$. Da definição de $V$ reconhece-se que $V$ não possui pontos com $x=y=0$ pelo que $DF$ é sobrejectiva em todos os pontos de $V$. Assim $V$ é uma variedade diferenciável de dimensão $1$.

   As linhas de $J_F\left(\frac{1}{\sqrt{6}},0,\frac{1}{3}\right)$ formam uma base para o espaço normal a $V$ em $\left(\frac{1}{\sqrt{6}},0,\frac{1}{3}\right)$. Tal permite identificar o espaço tangente no mesmo ponto como sendo formado por todos os vectores da forma $(0,\lambda,0)$ com $\lambda\in\mathbb{R}$.

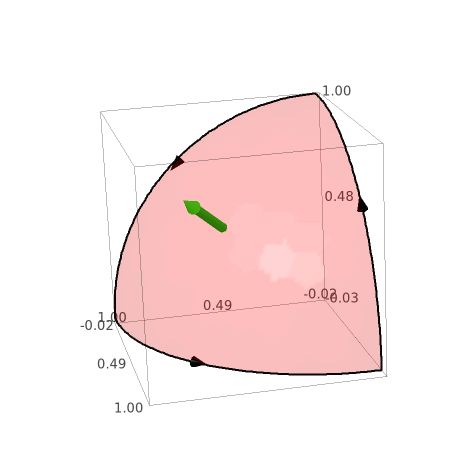
6. Calcule \[\iint_{S}\rot F\cdot\nu \, dS \] em que \[S=\{(x,y,z)\in\mathbb {R}^3:x > 0, y>0, z>0, x^2+y^2+z^2=1\},\] $\nu$ é a respectiva normal unitária contínua verificando $\nu(x,y,z)\cdot (0,0,1)>0$ para todo o $(x,y,z)\in S$ e $F(x,y,z)=(x\cos(yz),y\cos(xz),z(1-xy) )$.

   Solução

   Vamos aplicar o teorema de Stokes para calcular o integral.

   A superfície $S$ é um oitavo de esfera centrada na origem e de raio $1$ cujo bordo é formado por três arcos de circunferência cada um dos quais contido num plano coordenado e percorrido como sugerido pela figura.

   

   O teorema de Stokes permite escrever \[\iint_{S}\rot F\cdot\nu \, dS=\int_{L_1} F\cdot d\alpha + \int_{L_2} F\cdot d\beta + \int_{L_3} F\cdot d\gamma\] em que $\alpha(t)=(\cos t, \sen t, 0)$, $t\in [0,\pi/2]$, $L_1=\alpha([0,\pi/2])$, $\beta(t)=(0, \cos t, \sen t)$, $t\in [0,\pi/2]$, $L_2=\beta([0,\pi/2])$, $\gamma(t)=(\sen t, 0 , \cos t)$, $t\in [0,\pi/2]$, $L_3=\gamma([0,\pi/2])$.

   Acontece que todos os integrais de linha são $0$ pois sobre $L_1$ temos $F(x,y,z)=(x,y,0)$ e $\alpha'(t)=(-\sen t, \cos t, 0)$ donde $F(\alpha(t))\cdot\alpha'(t)= 0$ e analogamente nos restantes dois casos (em termos geométricos elementares isto corresponde à restrição de $F$ aos três arcos de circunferência ser uma função radial e portanto ortogonal à tangente ao arco de circunferência).

   Conclui-se assim que \[\iint_{S}\rot F\cdot\nu \, dS=0.\]