Solução do 2º Teste, versão A, 2014/15, 2º semestre
Enunciado
- Justifique que a equação $x+y^2+z^2+ e^{xyz}=2$ define implicitamente $z$ como uma função $h(x,y)$ numa vizinhança de $(x,y,z)=(0,0,1)$ e calcule $\frac{\partial h}{\partial x}(0,0)$.
- Calcule o volume de $V=\left\{(x,y,z)\in\mathbb{R}^3: x^2+y^2\leq 1, \frac{1}{2}\leq z\leq \sqrt{x^2+y^2}\right\}$.
- Seja $A=\{(x,y)\in\mathbb{R}^2: 1 \leq xy^2\leq 8, 1 \leq x^2 y\leq 8\}$ e $f:\mathbb{R}\to\mathbb{R}$ uma função contínua. Aplique a mudança de variável \[ \begin{cases}u=x y^2 \\ v=x^2 y \end{cases}\] para transformar o integral $\iint_A x^2 y^2 f(x^3 y^3)\,dx\, dy$ num integral de uma função adequada num intervalo de $\mathbb{R}^2$.
- Calcule o integral de linha $\int_L ye^{xy}\, dx +x e^{xy}\, dy$ em que $L$ é descrita por um caminho $C^1$ unindo a origem a um ponto $(a,b)$ verificando $ab=1$.
- Sejam $M=\{(x,y,z)\in\mathbb{R}^3: (x^2+y^2-1)(x^2+z^2-1)=0\}$ e
$E=\{(x,y,z)\in\mathbb{R}^3: x^2+y^2-1=0, x^2+z^2-1=0\}$.- Justifique que $M\setminus E$ é uma variedade bidimensional.
- Determine o espaço tangente e o espaço normal a $M\setminus E$ no ponto $(1,0,1)$.
- Calcule \[\iint_{\partial D}F\cdot\nu \, dS \] em que \[D=\{(x,y,z)\in\mathbb{R}^3:x > 0, y>0, z>0, x+y+z<1\},\] $\nu$ é a respectiva normal unitária exterior e $F(x,y,z)=(x+e^{y^2+z^2},y+e^{z^2+x^2},z+e^{x^2+y^2} )$.
Soluções
-
Seja $F:\mathbb{R}^3\to\mathbb{R}$ definida por $F(x,y,z)=x+y^2+z^2+ e^{xyz}-2$. Esta função é de classe $C^\infty(\mathbb{R}^3)$, $F(0,0,1)=0$ e a matriz jacobiana de $F$ é \[J_F(x,y,z)=\begin{bmatrix}1+yze^{xyz} & 2y+xze^{xyz} & 2z+xye^{xyz} \end{bmatrix}.\] Em particular, \[J_F(0,0,1)=\begin{bmatrix}1 & 0 & 2 \end{bmatrix}\] e $\frac{\partial F}{\partial z}(0,0,1)=2\neq 0$, pelo que o teorema da função implícita permite afirmar que a equação define $z$ como uma função de $x$ e $y$, $h(x,y)$, para $(x,y,z)$ num vizinhança de $(0,0,1)$.
Como $F(x,y,h((x,y))=0$ nessa vizinhança obtemos por diferenciação da igualdade anterior em ordem a $x$ \[\frac{\partial F}{\partial x}+\frac{\partial F}{\partial z} \frac{\partial h}{\partial x}=0\] donde \[\frac{\partial F}{\partial x}(0,0,1)+\frac{\partial F}{\partial z} (0,0,1)\frac{\partial h}{\partial x}(0,0)=0\] e, substituindo os valores das derivadas parciais de $F$ já conhecidos, \[\frac{\partial h}{\partial x}(0,0)=-1/2.\]
-
A descrição da região $V$ só depende de $\sqrt{x^2+y^2}$ e de $z$, o que permite identificá-la como sendo obtida por rotação em torno do eixo dos $zz$s. Assim, introduzimos $r=\sqrt{x^2+y^2}$ e reescrevemos as condições definindo a região como sendo \begin{gather*}r\leq 1 \\ \frac{1}{2}\leq z\leq r\end{gather*} que se devem verificar simultaneamente.
Esboçando no semi-plano $rz$ estas condições, obtemos
Determinando a região $V$ por rotação em torno do eixo dos $zz$s: esboço no semiplano $rz$ em que $r=\sqrt{x^2+y^2}$.
Embora não seja estritamente necessário fazer este esboço ou equivalente para resolver a questão, tal é fortemente recomendado.o que corresponde após rotação em torno do eixo dos $zz$s a
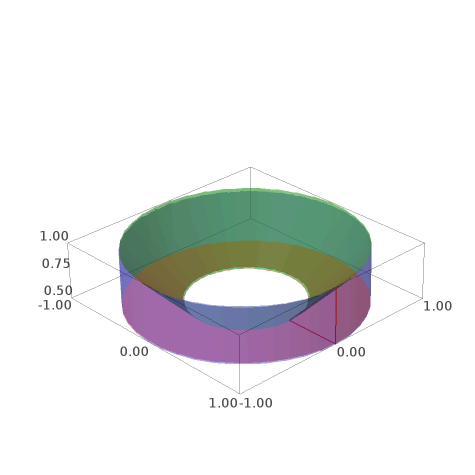
Animação produzida com Sage via Jmol do conjunto definido em $\mathbb{R}^3$ por $x^2+y^2\leq 1$, $\frac{1}{2}\leq z\leq \sqrt{x^2+y^2}$. Assim o volume da região $V$ será, usando coordenadas cilíndricas, \begin{align*}\iiint_V 1\, dx\, dy\, dz &= \int_0^{2\pi}\left(\int_{\frac{1}{2}}^1 \left(\int_{\frac{1}{2}}^r r \, dz\right)dr \right)d\theta\\ &=2\pi \int_{\frac{1}{2}}^1 \left( r^2 - {\frac{r}{2}}\right)dr = 2\pi \left( \frac{1}{3}-\frac{1}{24}-\frac{1}{4}+ \frac{1}{16}\right)=\frac{5\pi}{24}.\end{align*}
-
Consideremos a mudança de variável $g(x,y)=(u,v)=(xy^2, x^2y)$. Tem-se $g(A)=B=[1,8]\times[1,8]$ e \[ \det \frac{\partial(g_1,g_2)}{\partial(x,y)}=\det \begin{bmatrix}y^2 & 2xy \\ 2xy&x^2\end{bmatrix}=-3x^2y^2 \] e, portanto, \[\left| \det \frac{\partial(x,y)}{\partial(u,v)}\right|=\frac{1}{3x^2y^2}.\] Então, com $F(x,y)=x^2 y^2 f(x^3 y^3)$, \begin{align*}\iint_A x^2 y^2 f(x^3 y^3)\,dx\, dy &=\iint_B F(g^{-1}(u,v))\left| \det \frac{\partial(x,y)}{\partial(u,v)}\right|\,du\, dv \\ &=\frac{1}{3}\int_1^8 \int_1^8 f(uv)\,du\, dv.\end{align*}
-
Tomemos $F(x,y)= (ye^{xy}, xe^{xy})$. $F$ é uma função definida em $\mathbb{R}^2$, de classe $C^\infty(\mathbb{R}^2)$.
Alternativa 1
Seja $\phi:\mathbb{R}^2\to\mathbb{R}$ definida por $\phi(x,y)=e^{xy}$. Temos $\phi\in C^\infty(\mathbb{R}^2)$ e $F=\nabla \phi$. Assim, o campo vectorial $F$ é conservativo. Portanto \[\int_L ye^{xy}\, dx +x e^{xy}\, dy=\phi(a,b)-\phi(0,0)=e^{ab}-e^0=e-1.\]Alternativa 2
Como $\frac{\partial}{\partial y}(ye^{xy})=e^{xy}+xye^{xy}=\frac{\partial}{\partial x}(xe^{xy})$ podemos afirmar que $F$ é um campo fechado em $\mathbb{R}^2$ que é um conjunto em estrela. Logo $F$ é conservativo e o respectivo integral de linha é independente do caminho. Podemos considerar como caminho unindo $(0,0)$ a $(a,b)$ um segmento de recta parametrizado por $\alpha(t)=(ta,tb)$, $t\in [0,1]$. Então $\alpha'(t)=(a,b)$ e \[\int_L ye^{xy}\, dx +x e^{xy}\, dy=\int_0^1 2abt e^{abt^2} \, dt = e^{ab}-1 = e - 1.\] -
-
Alternativa A
Seja $F:\mathbb{R}^3\to\mathbb{R}$ dada por $F(x,y,z)=(x^2+y^2-1)(x^2+z^2-1)$; tem-se $F\in C^1(\mathbb{R}^3)$ e $M=\{(x,y,z)\in\mathbb{R}^3: F(x,y,z)=0\}.$ Quanto à matriz jacobiana de $F$, \[J_F= \begin{bmatrix}2x(x^2+y^2-1+x^2+z^2-1) & 2y(x^2+z^2-1) & 2z(x^2+y^2-1)\end{bmatrix},\] terá característica $1$ sse uma das suas entradas for não nula. Ora, se $(x,y,z) \in M\setminus E$, tem-se $x^2+z^2-1\neq 0$ ou $x^2+y^2-1\neq 0$. Se forem ambos não nulos, $\nabla F=(0,0,0)$ sse $(x,y,z)=(0,0,0)$, mas $(0,0,0) \not \in M$. Suponhamos, então que $x^2+y^2-1= 0$ (logo $x^2+z^2-1\neq 0$ ); ter-se-á $\frac{\partial F}{\partial z}=0$ e $\frac{\partial F}{\partial y}=\frac{\partial F}{\partial x}=0$ sse $x=y=0$, logo $x^2+y^2-1=-1= 0$, o que é absurdo. De modo análogo, também $x^2+z^2-1= 0$ conduz a um absurdo. Concluímos assim que a matriz jacobiana de $F$ tem característica igual a $1$ em todo o $(x,y,z) \in M\setminus E$.$M\setminus E$ é pois uma variedade de dimensão $2$.
Alternativa B
$M$ é formado por zeros das funções $(x,y,z)\mapsto \psi(x,y,z)=x^2+y^2-1$ e $(x,y,z)\mapsto \varphi(x,y,z)=x^2+z^2-1$. $E$ é formado pelos zeros simultâneos de $\psi$ e $\varphi$. $M\setminus E$ é formado pelos pontos de $M$ que não estão em $E$, ou seja, que não são zeros simultâneos de $\psi$ e $\varphi$.Em termos geométricos elementares $M$ é formado pela união dos cilindros de equações $x^2+y^2-1=0$ e $x^2+z^2-1=0$, $E$ é formado pela intersecção daqueles cilindros.
Para cada ponto de $M\setminus E$ existe um aberto $U$ que o contém tal que em $(M\setminus E)\cap U$ uma das funções $\psi$ ou $\varphi$ é não nula e a outra é identicamente nula (tal decorre da continuidade destas funções). Suponhamos concretamente que é aí $\psi=0$ e $\varphi\neq 0$. Então, em $U$, $M\setminus E$ coincide com os zeros de $\psi$. Bastará enão provar que $x^2+y^2-1=0$ define uma variedade $2$. Tal segue de $\psi$ ser $C^\infty$ e $J_\psi(x,y,z)=\begin{bmatrix}2x & 2y & 0\end{bmatrix}$ e uma das entradas desta matriz ter de ser não nula devido à condição $x^2+y^2=1$. O caso em que $\psi\neq 0$ e $\varphi= 0$ em $U$ é análogo.
-
Com a notação da alínea anterior, $\nabla F(1,0,1)=(2,0,0)$ (Alternativa A) ou $\nabla \psi(1,0,1)=(2,0,0)$ (Alternativa B) é vector normal à variedade no ponto $(1,0,1)$; o respectivo espaço normal é $\{(x,0,0): x \in\mathbb{R}\}$, isto é, a recta $y=z=0$.
Se $T$ é vector tangente a $M\setminus E$ no ponto $(1,0,1)$, tem-se $T \dot e_1=0$ e o espaço tangente é o espaço vectorial gerado por $e_2$ e $e_3$ , isto é, $\{(0,y,z): y,z \in\mathbb{R}\}=\{(x,y,z): x =0\}$.
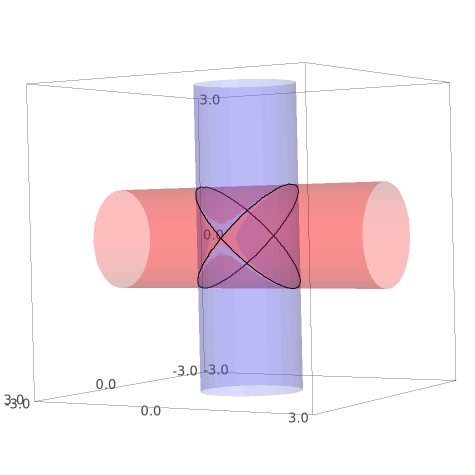
Os conjuntos $M$ (a união dos dois cilindros) e $L$ (a união das duas elipses a negro).
A imagem é apresentada a título ilustrativo. Não era necessário esboçar os conjuntos para resolver a questão.
-
-
Dado que $\div F=3$ o teorema da divergência permite obter \begin{align*}\iint_{\partial D} F\cdot \nu\, dS & = \iiint_D \div F \, dx\, dy\, dz \\ &= \int_0^1\left(\int_0^{1-x}\left(\int_0^{1-x-y}3\, dz\right) dy\right)dx \\ & = 3\int_0^1\left(\int_0^{1-x} 1-x-y\; dy\right)dx \\ &= 3 \int_0^1 (1-x)^2 - \frac{(1-x)^2}{2}\, dx = \frac{1}{2}. \end{align*}
Última edição desta versão: João Palhoto Matos, 24/03/2016 21:49:02.

