Sugestões... Soluções

Solução do 1º Teste, versão A, 2019/04/13

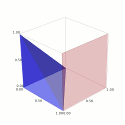
1. 1. Calcule o volume de $V=\{(x,y,z)\in \mathbb{R}^3:0\leq z \leq \sqrt{1-x}, y+z\leq 1, y\in [0,1], x\geq 0\}$.

      Solução

      1ª versão

      \begin{split} \iiint_V 1\, dx\, dy\, dz = \int_0^1\left(\int_0^{1-z}\left(\int_0^{1-z^2} 1 \, dx\right)\, dy\right)\, dz \\ = \int_0^1 z^3-z^2-z+1 \, dz = \frac{1}{4}-\frac{1}{3}-\frac{1}{2}+1=\frac{5}{12}.\end{split}

      2ª versão

      \[\iiint_V 1\, dx\, dy\, dz = \int_0^1\left(\int_0^{1-z^2}\left(\int_0^{1-z} \, dy\right)dx\right)dz=\dots = \frac{5}{12}.\]

      3ª versão

      [Integrando primeiro em ordem a $z$ conduz a cálculos mais extensos e não é recomendado mas também é possível.]

      A intersecção das superfícies $z=\sqrt{1-x}$ e $z+y=1$ é uma linha cuja projecção no plano $xy$ satisfaz $1-y = \sqrt{1-x}$ ou seja $x=1 - (1-y)^2=2y-y^2$.

      \begin{split}\iiint_V 1\, dx\, dy\, dz = \int_0^1\left(\int_{2y-y^2}^1\left(\int_0^{\sqrt{1-x}} \, dz \right)dx\right)dy \\ + \int_0^1\left(\int_0^{2y-y^2}\left( \int_0^{1-y} \, dz\right)dx\right)dy  = \dots= \frac{5}{12}.\end{split}

   2. Justifique que se pode inverter a ordem de integração para calcular \[\int_0^1 \left(\int_x^1 \sen\left(\frac{x}{t}\right)\, dt\right)dx\] e obtenha o valor do integral.

      Solução

      

      Seja $T=\{(t,x)\in\mathbb{R}^2: x\in [0,1], x\leq t\leq 1\}$ e considere-se a função $f:T\to \mathbb{R}$ definida por \[f(t,x)= \begin{cases}\sen\left(\frac{x}{t}\right), & \text{ se } t\gt 0, \\ 0, & \text{ caso contrário}.\end{cases}\] A função $f$ é limitada e é contínua excepto no ponto $(0,0)$ e portanto o conjunto dos seus pontos de descontinuidade tem medida nula. O conjunto $T$ tem fronteira com medida nula pois esta é formada por três segmentos de recta. Sendo assim $f$ é integrável em $T$ e o teorema de Fubini garante que \begin{align*}\iint_T f \, dx\, dt & = \int_0^1 \left(\int_x^1 \sen\left(\frac{x}{t}\right)\, dt\right)dx \\ & = \int_0^1 \left( \int_0^t \sen\left(\frac{x}{t}\right)\, dx\right)dt \\ & = \int_0^1 \left.\left[-t\cos\left(\frac{x}{t}\right)\right]\right|^{x=t}_{x=0}\,dt \\ & = \int_0^1 t-t\cos 1\, dt = \frac{1}{2}(1-\cos 1).\end{align*}

2. Considere uma função definida num subconjunto $D$ de $\mathbb{R}^2$ por \[f(x,y)=\frac{\sqrt{y-x}}{\log\left(1+\sqrt{1-x^2-y^2}\right)}\]

   1. Determine o domínio $D$ de $f$.
      Solução

      Notar que $\log\left(1+\sqrt{1-x^2-y^2}\right)$ está sempre definido desde que o argumento do logaritmo esteja definido, pois este é sempre $\geq 1$. Por sua vez $1+\sqrt{1-x^2-y^2}$ está definido para $1-x^2-y^2 \geq 0 \Leftrightarrow x^2+y^2 \leq 1$. Para $\log\left(1+\sqrt{1-x^2-y^2}\right)$ ser diferente de $0$, devemos ter \[1+\sqrt{1-x^2-y^2}\gt 1\Leftrightarrow 1-x^2-y^2 \gt 0 \Leftrightarrow x^2+y^2 \lt 1.\] Portanto \[D=\{(x,y)\in\mathbb{R}^2:y\geq x, x^2+y^2\lt 1\}.\]

      

   2. Determine $\operatorname{int} D$, $\partial D$ e $\overline{D}$ e decida se $D$ é aberto, fechado, conexo ou limitado.
      Solução

      \begin{align*}\operatorname{int} D & = \{(x,y)\in\mathbb{R}^2: x^2+y^2\lt 1, y\gt x\} , \\ \partial D & = \{(x,y)\in\mathbb{R}^2: x^2+y^2 = 1, y\geq x\} \cup \left\{(x,y)\in\mathbb{R}^2: y= x, |x| \leq \textstyle\frac{\sqrt{2}}{2} \right\}, \\ \overline{D}& = \{(x,y)\in\mathbb{R}^2: x^2+y^2 \leq 1, y\geq x\}.\end{align*} Como $D\neq \operatorname{int} D$, $D$ não é aberto. Como $D\neq \overline{D}$, $D$ não é fechado. Como $D\subset B_1(0,0)$, temos que $D$ é limitado. Para qualquer ponto $(x_0,y_0)\in D$ temos que o segmento de recta $\{(tx_0,ty_0): t\in [0,1]\}$ une o ponto a $(0,0)$ pelo que quaisquer dois pontos de $D$ pode ser unidos por um caminho. Assim $D$ é conexo por arcos e portanto conexo.

3. Considere a função $h:\mathbb{R}^2\to\mathbb{R}$ definida por \[h(x,y)=\begin{cases}\dfrac{x^5}{x^4 + y^4}, & \text{se $(x,y)\neq (0,0)$,}\\ 0, & \text{caso contrário.} \end{cases}\]

   1. Decida se $h$ é ou não contínua em $(0,0)$.
      Solução

      Temos \[|h(x,y)-h(0,0)|=\frac{|x|^5}{x^4+y^4}= |x|\frac{x^4}{x^4+y^4}\leq |x| \leq \sqrt{x^2+y^2} =|(x,y)-(0,0)|\] Assim, se $|(x,y)-(0,0)|\lt \epsilon$ também $|h(x,y)-h(0,0)|\lt \epsilon$, pelo que $h$ é contínua em $(0,0)$.

       

   2. Decida se $h$ é ou não diferenciável em $(0,0)$.
      Solução

      Temos \begin{align*}\frac{\partial h}{\partial x}(0,0) &= \lim_{\lambda\to 0}\frac{h(\lambda, 0)-h(0,0)}{\lambda} = \lim_{\lambda\to 0} \frac{\lambda^5}{\lambda \lambda^4}= 1, \\ \frac{\partial h}{\partial y}(0,0) &= \lim_{\lambda\to 0}\frac{h(0,\lambda)-h(0,0)}{\lambda} = \lim_{\lambda\to 0} \frac{0}{\lambda} = 0.\end{align*}

      Assim, verificar se $h$ é ou não diferenciável em $(0,0)$ corresponde a estabelecer se existe e é igual a $0$ \begin{align*}& \lim_{(x,y)\to (0,0)}\frac{1}{\sqrt{x^2+y^2}} (h(x,y)-h(0,0)-\nabla h(0,0)\cdot (x,y)) \\ & = \lim_{(x,y)\to (0,0)}\left(\frac{x^5 }{x^4+y^4}-x\right)\frac{1}{\sqrt{x^2+y^2}}  \\ & = \lim_{(x,y)\to (0,0)} \frac {-xy^4}{(x^4+y^4)\sqrt{x^2+y^2}}.\end{align*} Se neste limite considerarmos a restrição da função à recta $y=x$ obtemos \[\lim_{x\to 0}\frac{-x^5}{2\sqrt{2}|x|x^4}= \lim_{x\to 0} \frac{-x}{2\sqrt{2}|x|}\] que não existe, pelo que $h$ não é diferenciável em $(0,0)$.

4. Considere funções $F:\mathbb{R}^2\to\mathbb{R}$ com $F\in C^2(\mathbb{R}^2)$ e $G:\mathbb{R}^2\to\mathbb{R}$  definida por \[G(x,y)=F(x\cos y,x \sen y).\] Calcule, em termos de derivadas parciais adequadas de $F$:

   1. A derivada dirigida $D_{(1,-1)}G\left(1,\frac{\pi}{2}\right)$.
      Solução

      Seja $p:\mathbb{R}^2\to \mathbb{R}^2$ definida por $(u,v)=p(x,y)=(x\cos y, x\sen y)$. Trata-se de uma aplicação de classe $C^\infty(\mathbb{R}^2)$ e portanto diferenciável. $F$ é uma função de classe $C^2(\mathbb{R}^2)$ e portanto diferenciável e com derivadas parciais diferenciáveis. Podemos então usar o teorema de derivação da função composta para justificar que $G$ é uma função diferenciável com $DG(x,y)=DF(p(x,y))Dp(x,y)$ pelo que \begin{align}\frac{\partial G}{\partial x} & = \frac{\partial F}{\partial u}(x\cos y, x\sen y) \cos y + \frac{\partial F}{\partial v}(x\cos y, x\sen y) \sen y \notag \\ \frac{\partial G}{\partial y}  & = - \frac{\partial F}{\partial u}(x\cos y, x\sen y) x \sen y + \frac{\partial F}{\partial v}(x\cos y, x\sen y) x\cos y \label{eq2}\end{align}

      Como $G$ é diferenciável \begin{align*}D_{(1,-1)}G\left(1,\frac{\pi}{2}\right) & = \nabla G\left(1,\frac{\pi}{2}\right) \cdot (1,-1) \\ &= \frac{\partial G}{\partial x} \left(1,\frac{\pi}{2}\right) - \frac{\partial G}{\partial y} \left(1,\frac{\pi}{2}\right) \\ & = \frac{\partial F}{\partial v}(0, 1) + \frac{\partial F}{\partial u}(0, 1). \end{align*}

   2. $\frac{\partial^2 G}{\partial x\partial y}\left(1,\frac{\pi}{2}\right)$.
      Solução

      Usando de novo o teorema de derivação da função composta e a identidade $(\ref{eq2})$ obtemos \begin{align*}\frac{\partial^2 G}{\partial x\partial y} = & \frac{\partial}{\partial x}\left(\frac{\partial G}{\partial y}\right)\\   = & - \frac{\partial F}{\partial u}(x\cos y, x\sen y) \sen y + \frac{\partial F}{\partial v}(x\cos y, x\sen y) \cos y  \\ & - \frac{\partial^2 F}{\partial u^2} (x\cos y, x\sen y) x\sen y \cos y - \frac{\partial^2 F}{\partial v \partial u} (x\cos y, x\sen y) x\sen^2 y \\ & +\frac{\partial^2 F}{\partial u \partial v} (x\cos y, x\sen y) x\cos^2 y +\frac{\partial^2 F}{\partial  v^2} (x\cos y, x\sen y) x\sen y \cos y\end{align*} pelo que \[\frac{\partial^2 G}{\partial x\partial y} \left(1, \frac{\pi}{2}\right) = - \frac{\partial F}{\partial u}(0, 1) - \frac{\partial^2 F}{\partial v \partial u} (0, 1). \]

5. Seja $\psi:\mathbb{R}\to\mathbb{R}$ definida por \[\psi(x)=\int_0^1 \dfrac{e^{-t}}{t+1}\sen((t+1)x)\, dt.\] Justifique que $\psi$ é diferenciável e calcule $\psi'(0)$.

   Solução

   A função $(t,x)\mapsto \dfrac{e^{-t}}{t+1}\sen((t+1)x)$ é de classe $C^1$ num aberto contendo $[0,1]\times \mathbb{R}$ pelo que para todo o $x\in\mathbb{R}$ temos que $\psi$ é diferenciável com \[\psi'(x)=\int_0^1 \frac{\partial}{\partial x}\left(\frac{e^{-t}}{t+1}\sen((t+1)x)\right)\, dt= \int_0^1 e^{-t}\cos((t+1)x)\, dt.\] Em particular \[\psi'(0)=\int_0^1 e^{-t}\, dt =1-e^{-1}.\]

6. Seja $g:\mathbb{R}^2\to \mathbb{R}$ definida por $g(x,y)=e^{x^2+y^2}-4xy-y^4$.

   1. Decida se $(0,0)$ é um ponto de máximo local, um ponto de mínimo local, ou um ponto de sela de $g$.
      Solução

      Temos \begin{align*}\frac{\partial g}{\partial x} & = 2x e^{x^2+y^2} - 4y \\ \frac{\partial g}{\partial y} & = 2y e^{x^2+y^2} -4x -4 y^3\end{align*} pelo que $(0,0)$ é um ponto de estacionaridade de $g$.

      Adicionalmente \begin{align*}\frac{\partial^2 g}{\partial x^2} & = (2 + 4x^2) e^{x^2+y^2} \\ \frac{\partial^2 g}{\partial y^2} & = (2+ 4y^2) e^{x^2+y^2}  -12 y^2 \\ \frac{\partial^2 g}{\partial x \partial y} & = 4xy e^{x^2+y^2} - 4 \end{align*}

      Assim a matriz hessiana de $g$ em $(0,0)$ é \[H_g(0,0)=\begin{bmatrix} 2 & -4 \\ -4 & 2\end{bmatrix}\] O determinante desta matriz é negativo, portanto a forma quadrática associada é indefinida e $(0,0)$ é um ponto de sela.

   2. Mostre que $g$ possui um ponto de mínimo absoluto.
      Solução

      Temos $g(x,y)\geq e^{x^2+y^2} - 2 (x^2+y^2) - (x^2 + y^2)^2$. Como $\lim_{t\to \infty} e ^{t^2}- 2t^2 - t^4= +\infty$ temos \[\lim_{(x,y)\to \infty} g(x,y)= +\infty.\] Assim podemos afirmar que existe uma bola $B_r(0,0)$ tal que $g(x,y)\geq 2$ em $\mathbb{R}^2\setminus B_r(0,0)$.

      Como $\overline{B}_r(0,0)$ é limitado e fechado, o teorema de Weierstrass garante que $g$ tem um mínimo em $\overline{B}_r(0,0)$. Como $g(0,0)=1$ temos que esse mínimo é menor ou igual a $1$. Portanto ocorrerá num ponto interior de $\overline{B}_r(0,0)$ e é um mínimo absoluto de $g$ em $\mathbb{R}^2$.

       

A definição do conjunto $V$ na pergunta 1.a estava incompleta faltando $0\leq z$ (e de forma análoga na versão B). Tal não foi detectado durante a prova pelos professores e não foi objecto de pedidos de esclarecimento pelos alunos (foi detectado pelo último aluno a entregar a prova). A situação irá ser avaliada em função das respostas que foram de facto apresentadas e serão tomadas medidas de compensação ao nível da classificação em função dessa avaliação. Em princípio, tanto respostas em que foi assumido o psicologicamente natural $0\leq z$, ou que denotem problemas motivados pela falta dessa condição, poderão atingir a classificação de 100%. A única resposta de facto integralmente correcta que poderia ser dada, que consiste em afirmar que o problema era insolúvel devido ao conjunto ser ilimitado, também terá evidentemente cotação de 100%.