Solução das repetições de testes e exame, 2021/07/07
Detalhes adicionais poderão ser adicionados durante o processo de revisão de provas se necessário.
1º Teste
-
- Calcule, usando mudança de ordem de integração, \[
\int_0^{1/2}\left(\int_0^1 (y^2+1)e^{x(y^2+1)}\, dy\right) dx + \int_{1/2}^1\left(\int_0^{\sqrt{\frac{1}{x}-1}} (y^2+1)e^{x(y^2+1)}\, dy\right) dx.\] - Calcule o volume de $V=\left\{(x,y,z)\in\mathbb{R}^3:x+y^2\leq z\leq \frac{x+1}{2}+ \frac{y^2}{2}, x\geq 0\right\}$.
Solução
A projecção de $V$ no plano $xy$ é determinada por \[\begin{cases}x+y^2\leq \frac{x+1}{2}+ \frac{y^2}{2}, \\ x\geq 0.\end{cases}\] A primeira condição é equivalente a $\frac{x-1}{2}\leq - \frac{y^2}{2}\Leftrightarrow x\leq 1 -y^2$. Portanto a projecção de $V$ no plano $xy$ é caracterizada por $0\leq x\leq 1 -y^2$. Assim o volume de $V$ é dado por \begin{align*}\int_{-1}^1\left(\int_0^{1-y^2}(y^2-x+1)\, dx \right)dy & = \frac{1}{2} \int_{-1}^1 (1-y^2)(y^2+1)- \frac{(1-y^2)^2}{2}\, dy.\\ & = \frac{1}{2} \int_{-1}^1 \frac{1}{2}+y^2 - \frac{3y^4}{2}\, dy \\ & = \frac{1}{2}\left(1+\frac{2}{3}-\frac{3}{5}\right) = \frac{1}{3}.\end{align*}
- Calcule, usando mudança de ordem de integração, \[
- Decida se a função $\phi:\mathbb{R}^2\to \mathbb{R}$ definida por \[\phi(x,y)=\begin{cases}\frac{y \arctg(x)}{\sqrt{x^2+y^2}}, & \text{se $(x,y)\neq (0,0)$}, \\ 0, & \text{se $(x,y)=(0,0)$,}\end{cases}\] é ou não:
- contínua em $(0,0)$.
Solução
Como $|\phi(x,y)-\phi(0,0)|\leq \frac{|y|}{|\arctg(x)|}{\sqrt{x^2+y^2}}\leq |\arctg(x)|$, a continuidade do $\arctg$ em $0$ com valor $0$ implica a continuidade de $\phi$ em $(0,0)$.
- diferenciável em $(0,0)$.
Solução
Como $\phi$ é identicamente nula sobre os eixos coordenados, temos \[\frac{\partial \phi}{\partial x}(0,0)=\frac{\partial \phi}{\partial y}(0,0)=0.\] Portanto diferenciabilidade em $(0,0)$ corresponderia a \[\lim_{(x,y)\to(0,0)}\frac{y\arctg x}{x^2+y^2}= 0.\] Acontece que este limite não é $0$ pois \[\lim_{\stackrel{(x,y)\to(0,0)}{y=x}}\frac{y\arctg x}{x^2+y^2}=\lim_{x\to 0}\frac{\arctg x}{2x}=\frac{1}{2}.\]
Portanto $\phi$ não é diferenciável em $(0,0)$.
- contínua em $(0,0)$.
- Seja $G:\mathbb{R}^2\to\mathbb{R}$ uma função de classe $C^2(\mathbb{R}^2)$ e considere uma função definida por $F(x,y)=G(xy, \log x \log y)$.
- Exprima $\nabla F$ em termos de $\nabla G$.
- Exprima $\frac{\partial^2 F}{\partial x\partial y}(1,1)$ em termos de derivadas parciais adequadas de $G$.
Sugestão
Ver uma questão similar no 1º teste deste ano.
- Considere a função $h:\mathbb{R}^2 \to \mathbb{R}$ definida por $h(x,y)=e^{xy}(1-x^2-y^2)$.
- Obtenha a expressão da derivada dirigida $D_{(-x,y)}h(x,y)$.
Solução
\begin{align*}\frac{\partial h}{\partial x} & = e^{xy}[y(1-x^2-y^2)-2x]\\ \frac{\partial h}{\partial y} & = e^{xy}[x(1-x^2-y^2)-2y]\end{align*}\[D_{(-x,y)}h(x,y)=-x\frac{\partial h}{\partial x}+y\frac{\partial h}{\partial y}=2e^{xy}(x^2-y^2).\]
- Use o cálculo da alínea anterior para mostrar que se $(a,b)$ é um ponto de estacionaridade de $h$ então $|a|=|b|$.
Solução
Num ponto de estacionaridade de uma função diferenciável todas as derivadas dirigidas são nulas e, em particular, a derivada dirigida calculada na alínea anterior. Daí que $x^2-y^2=0 \Leftrightarrow |x| = |y|$.
- Determine todos os pontos de estacionaridade de $h$.
Solução
Da alínea anterior sabemos que eventuais pontos de estacionaridade situam-se sobre a recta $y=x$ ou sobre a recta $y=-x$.
Na recta $y=x$ o sistema de estacionaridade reduz-se à equação \[-e^{x^2}(x+x^3)=0\] cuja única solução é $x=0$. Assim, o único ponto de estacionaridade sobre esta recta é $(0,0)$.
Na recta $y=-x$ obtém-se de forma análoga \[-e^{-x^2}(3x-2x^3)=0\] que tem três soluções: $x=0$, $x=\sqrt{\frac{3}{2}}$ e $x=-\sqrt{\frac{3}{2}}$. Isto fornece-nos mais dois pontos de estacionaridade: $\left(\sqrt{\frac{3}{2}}, -\sqrt{\frac{3}{2}}\right)$ e $\left(-\sqrt{\frac{3}{2}}, \sqrt{\frac{3}{2}}\right)$.
- Decida se $h$ possui ou não um máximo absoluto e, se optar pela afirmativa, determine o seu valor e onde ocorre.
Solução
Note-se que $h\gt 0$ em $B_1(0,0)$, $h=0$ em $\partial B_1(0,0)$ e $h\lt 0$ em $\mathbb R^2\setminus \overline{B}_1(0,0)$.
Por aplicação do teorema de Weierstrass sabemos que a restrição de $h$ a $\overline{B}_1(0,0)$ terá um máximo. Como este terá que ser positivo, ocorrerá num ponto interior, isto é, em $B_1(0,0)$. Esse máximo ocorrerá num ponto de estacionaridade. Como o único ponto de estacionaridade em $B_1(0,0)$ é $(0,0)$, este será o ponto de máximo, valendo o máximo $h(0,0)=1$. Como $h$ toma valores negativos em $\mathbb R^2\setminus \overline{B}_1(0,0)$, este máximo é absoluto.
- Determine o contradomínio de $h$.
Solução
Usando o teorema do valor intermédio, o resultado da alínea anterior, e $\lim_{x\to +\infty}h(x,x)=\lim_{x\to +\infty} e^{x^2}(1-2x^2)= -\infty$, conclui-se que $h(\mathbb R^2)={]-\infty, 1]}$.
- Obtenha a expressão da derivada dirigida $D_{(-x,y)}h(x,y)$.
- Determine um polinómio $p(x,y)$ tal que \[\lim_{(x,y)\to (0,0)}\frac{\sen(x+2xy)-p(x,y)}{x^2+y^2}=0.\]
Sugestão
Fórmula de Taylor de 2ª ordem.
2º Teste
- Considere o sistema \[\begin{cases}z - w = x - y + e^{xy} \\ z+w = x+y +\cos(xy).\end{cases}\]
- Mostre que o sistema define $(x,y)$ como função de $(z,w)$, numa vizinhança de $(x,y,z,w)=(0,0,1,0)$.
Sugestão
Teorema da função implícita.
- Calcule $\frac{\partial y}{\partial z}(1,0)$.
Solução
Considerando que $(x,y)$ é função $C^1$ de $(z,w)$ como estabelecido na alínea anterior e diferenciando ambas as equações em ordem a $z$ obtém-se \begin{align*}1 &=\frac{\partial x}{\partial z} -\frac{\partial y}{\partial z}+e^{xy}\left(x\frac{\partial y}{\partial z}+y\frac{\partial x}{\partial z}\right) \\ 1 & = \frac{\partial x}{\partial z} +\frac{\partial y}{\partial z} -\sen(xy) \left(x\frac{\partial y}{\partial z}+y\frac{\partial x}{\partial z}\right)\end{align*} donde em $(x,y,z,w)=(0,0,1,0)$ temos \begin{align*}1 &=\frac{\partial x}{\partial z}(1,0) -\frac{\partial y}{\partial z}(1,0) \\ 1 & = \frac{\partial x}{\partial z}(1,0) +\frac{\partial y}{\partial z}(1,0)\end{align*} pelo que $\frac{\partial y}{\partial z}(1,0)=0$.
- Mostre que o sistema define $(x,y)$ como função de $(z,w)$, numa vizinhança de $(x,y,z,w)=(0,0,1,0)$.
- Calcule a área da superfície $S=\{(x,y,z)\in\mathbb{R}^3: x^2+y^2=1, 0\leq z\leq x, y\geq 0\}$.
Solução
A superfície pode ser parametrizada por $r(\theta, z)=(r\cos \theta, r\sen\theta, z)$ com $(\theta, z)$ com $\theta\in [0,\frac{\pi}{2}]$ e $z\in [0,\cos \theta]$. O elemento de volume bidimensional para esta parametrização é \[\left\|\frac{\partial r}{\partial \theta}\times \frac{\partial r}{\partial z}\right\| = \| (-\sen\theta , \cos\theta, 0)\times (0,0,1)\|=\|(\cos\theta, \sen \theta , 1)\|=1\] pelo que a área é dada por \[\int_0^{\frac{\pi}{2}}\left(\int_0^{\cos\theta}1\, dz\right)\,d\theta=1.\]
- Seja $V=\{(x,y,z)\in\mathbb{R}^3:-1+\sqrt{x^2+y^2}\leq z\leq \frac{x^2+y^2}{4},{\color{red}{z\leq 1}}\}$. Calcule o valor de \[\iiint_V z\, dx\, dy\, dz\]
Solução
A descrição de $V$ apareceu incompleta no enunciado faltando o que está indicado a vermelho. A única resposta totalmente correcta possível é o integral não existe. Respostas com um mínimo de senso terão cotação completa.
- Considere o integral de linha \[\int_L \frac{y}{x^2+y^2}dx - \frac{x}{x^2+y^2}dy\] em que $L$ é definida por $\alpha(t)=\begin{cases}(1, t), \text{se $t\in [0,1]$,}\\ (2-t, 1), \text{se $t\in [1,2]$.}\end{cases}$.
- Calcule o valor do integral.
Solução
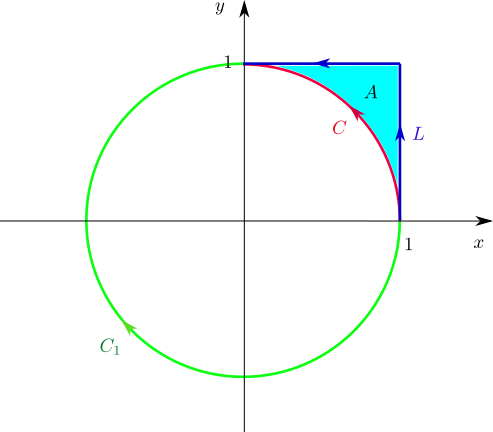
Usando o teorema de Green para calcular $\int_L \frac{y}{x^2+y^2}\, dx - \frac{x}{x^2+y^2}\, dy$. [O curso forneceu vários métodos que podem ser usados para atacar este problema: cálculo directo, existência de potenciais de campos fechados em abertos em estrela, invariância de integrais de linha de campos fechados entre caminhos homotópicos, teorema de Green. Note-se que o simétrico do campo também apareceu em vários exemplos que considerámos. A solução apresentada está longe de ser única.]
Seja $A=\{(x,y)\in[0,1]^2 : x^2+y^2\geq 1\}$ e $C$ a linha definida pelo caminho $\alpha(t)=(\cos t, \sen t)$, $t\in \left[0,\frac{\pi}{2}\right]$. Então por aplicação do teorema de Green \begin{align*}\int_L \frac{y}{x^2+y^2}\, dx - \frac{x}{x^2+y^2}\, dy & = \iint_A \frac{\partial}{\partial x}\left(- \frac{x}{x^2+y^2}\right) - \frac{\partial}{\partial y} \left(\frac{y}{x^2+y^2}\right)\, dx\, dy \\ & \qquad + \int_C \frac{y}{x^2+y^2}\, dx - \frac{x}{x^2+y^2}\, dy \\ & = 0 + \int_0^{\pi/2} -1 \, dt = -\frac{\pi}{2}.\end{align*}
- Decida se é possível, substituindo o caminho por outro com o mesmo início e o mesmo fim, obter um valor distinto para o integral.
Solução
Considere-se o caminho $\beta(t)=(\cos t, -\sen t)$, $t\in \left[0, \frac{3\pi}{2}\right]$, $C_1=\beta([0, \frac{3\pi}{2}])$. Então \[\int_{C_1} \frac{y}{x^2+y^2}\, dx - \frac{x}{x^2+y^2}\, dy = \frac{3\pi}{2}.\]
- Calcule o valor do integral.
- Seja $\psi:\mathbb R^3\to \mathbb R^3$ definida por \[F(x,y,z)=(y(z^2-3),x(z^2-3),xyz)\] e considere a superfície \[S=\left\{(x,y,z)\in\mathbb{R}^3: x^2+y^2+z^2=4, x^2+y^2\geq 1 \right\}.\]
Calcule \[\iint_S \rot F\cdot \nu \, dS\] em que $\nu$ designa a normal unitária contínua sobre $S$ tal que $\nu(2,0,0)\cdot(1,0,0)\gt 0$.
Sugestão
Use o Teorema de Stokes. O bordo da superfície é constituído pelas circunferências de raio $1$ contidas nos planos horizontais $z=\sqrt{3}$ e $z=-\sqrt{3}$, centradas no eixo dos $z$s, e percorridas em sentidos apropriados.
Última edição desta versão: João Palhoto Matos, 13/07/2021 09:22:36.